Hello all, This post is all about Uniswap V2 Contracts. This is the notes written by me while learning Uniswap V2 from various resources. I have written short notes on each and every line of code in UniswapV2 Core Contracts and UniswapV2 Periphery Contracts. You can check my Uniswap V1_V2_V3 Overview post to get a an overview on Uniswap protocol.

I have used many resources to learn about UniswapV2. This notes aggregates Rareskills UniswapV2 Book, @0xOwneThurm, @ProgrammerSmart, @Zer0luck.eth, @officer_cia and few the great anons.

I am very grateful to all these legends for the knowledge

Chapter-1 : ERC4626 Vaults

ERC4626 is a tokenized vault standard that uses ERC20 tokens to represent shares of some other asset.

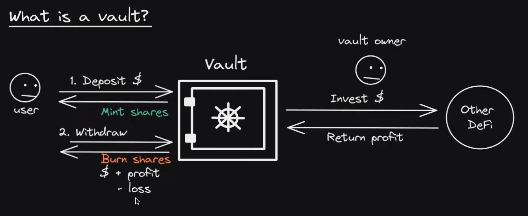
When an ERC4626 contract gives you an ERC20 token for the initial deposit, it gives you token S (an ERC20 compliant token). ERC4626 contract is also ERC20 token.

The ERC4626 extends the ERC20 contract and during construction phase, it takes as an argument the other ERC20 token users will be depositing to it. Therefore, ERC4626 supports all the functions and events you expect from ERC20. The token of ERC4626 contract is referred to shares.

Each ERC4626 contract only supports one asset. You cannot deposit multiple kinds of ERC20 tokens into the contract and get shares back.

Why ERC4626 ?

Let’s say we all own a company, or a liquidity pool, that earns a stablecoin DAI periodically. The stablecoin DAI is the asset in this case.

One inefficient way we could distribute the earnings is to push out DAI to each of the holders of the company on a pro-rata basis. But this would be extremely expensive gas wise.

Instead, this is how the workflow would work with ERC4626.

Let’s say you and ten friends get together and each deposit 10 DAI each into the ERC4626 vault. You get back one share.

So far so good. Now your company earns 10 more DAI, so the total DAI inside the vault is now 110 DAI.

When you trade your share back for your part of the DAI, you don’t get 10 DAI back, but 11.

Now there is 99 DAI in the vault, but 9 people to share it among. If they were to each withdraw, they would get 11 DAI each.

Note how efficient this is. When someone makes a trade, instead of updating everyones shares one-by-one, only the total supply of shares and the amount of assets in the contract changes.

Methods

https://ethereum.org/en/developers/docs/standards/tokens/erc-4626/

Giving assets, getting shares: deposit() and mint()

According to the EIP, the user is depositing assets and getting shares back, so what's the difference between these two functions?

• With deposit(), you specify how many assets you want to put in, and the function will calculate how many shares to send to you.
• With mint(), you specify how many shares you want, and the function will calculate how much of the ERC20 asset to transfer from you.

Of course, if you don’t have enough assets to transfer in to the contract, the transaction will revert.

The uint256 that gets returned to you is amount of shares you get back.

Anticipating how many shares you will get

• previewDeposit
• previewMint

Like their state changing counterparts, previewDeposit takes assets as an argument and previewMint takes shares as an argument.

Anticipating how many shares you will get under ideal conditions

Confusingly enough, there is also a view function called convertToShares which takes assets as an argument and returns the amount of shares you will get back under ideal conditions (no slippage or fees).

Why would you care about this ideal information that doesn’t reflect the trade you will execute?

The difference between ideal and actual results tells you how much your trade is impacting the market and how the fee depends on trade size. A smart contract could do a binary search on the difference between convertToShares and previewMint to find the best trade size to execute.

Returning shares, getting assets back The inverse of deposit and mint is withdraw and redeem respectively.

withdraw lets you specify how many assets you want to take from the contract, and the contract calculates how many of your shares to burn.

function withdraw(uint256 assets, address receiver, address owner) public returns (uint256 shares)

redeem, you specify how many shares you want to burn, and the contract calculates the amount of assets to give back.

function redeem(uint256 shares, address receiver, address owner) public returns (uint256 assets)

Anticipating how many shares you will burn to get assets back

The view methods for withdraw and redeem are previewRedeem and previewWithdraw respectively.

The idealized analog of these functions is convertToAssets which takes shares as an argument and gives you how many assets you will get back, not including fees and slippage.

Summary of functions :*

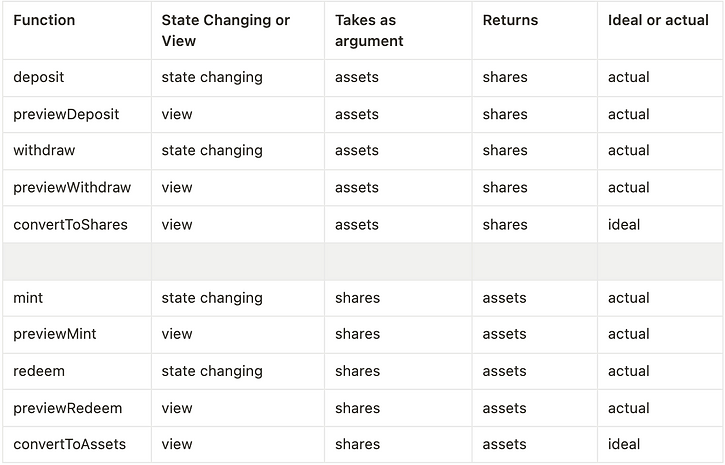
The functions mint, deposit, redeem, and withdraw, have an second argument “receiver” for cases where the account receiving shares or assets from the ERC4626 is not msg.sender. This means I can deposit assets into the account and specify that the ERC4626 contract give you the shares.

Redeem and withdraw have a third argument, “owner” which allows msg.sender to burn the shares of the “owner” while sending assets to the “receiver” (second argument) if they have allowance to do so.

maxDeposit, maxMint, maxWithdraw, maxRedeem These functions take identical arguments to their state-changing counterparts and return the largest trade they can execute. This can change per address (remember, we just discussed that these functions take addresses as arguments).

Events

ERC4626 has only two events in addition to the ERC20 events it inherits: Deposit and Withdraw. These are also emitted if mint and redeem were called, because functionally the same thing happened: tokens were swapped.

event Deposit(
    address indexed sender,
    address indexed owner,
    uint256 assets,
    uint256 shares
)
event Withdraw(
    address indexed sender,
    address indexed receiver,
    address indexed owner,
    uint256 assets,
    uint256 share
)

Slippage

Any token swapping protocol has an issue where the user might not get back the amount of tokens they were expecting.

For example, with automated market makers, a large trade might use up the liquidity and cause the price to move substantially.

Another issue is a transaction getting frontrun or experiencing a sandwich attack. In the examples above, we've assumed the ERC4626 contract maintains a one-to-one relationship between asset and shares regardless of the supply, but the ERC4626 standard does not dictate how the pricing algorithm should work.

For example, suppose we make the amount of shares issued a function of the square root of the assets deposited. In that case, whoever deposits first will get a larger amount of shares. This could encourage opportunistic traders to frontrun deposit orders and force the next buyer to pay a larger amount of the asset for the same amount of shares.

The defense against this is simple: the contract interacting with an ERC4626 should measure the amount of shares it received during a deposit (and assets during a withdraw) and revert if it does not receive the quantity expected within a certain slippage tolerance.

This is a standard design pattern to deal with slippage issues. It will also defend against the issue described below.

ERC4626 inflation attack

Although ERC4626 is agnostic to the algorithm that translates prices to shares, most implementations use a linear relationship. If there are 10,000 assets, and 100 shares, then 100 assets should result in 1 share.

But what happens if someone sends 99 assets? It will round down to zero and they get zero shares.

Of course no-one would intentionally throw away their money like this. However, an attacker can frontrun a trade by donating assets to the vault.

If an attacker donates money to the vault, one share is suddenly worth more than it was initially. If there are 10,000 assets in the vault corresponding to 100 shares, and the attacker donates 20,000 assets, then one share is suddenly worth 300 assets instead of 100 assets. When the victim’s trade trades in assets to get back shares, they suddenly get a lot fewer shares — possibly zero.

There are three defenses:

• Revert if the amount received is not within a slippage tolerance (described earlier)
• The deployer should deposit enough assets into the pool such that doing this inflation attack would be too expensive
• Add "virtual liquidity" to the vault so the pricing behaves as if the pool had been deployed with enough assets.

Here is OpenZeppelin's implementation of virtual liquidity:

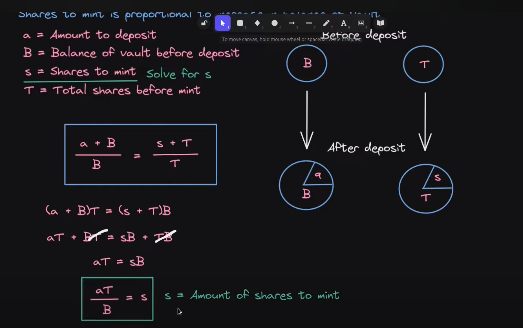
When calculating the amount of shares a depositor receives, the total supply is artificially inflated (at a rate the programmer specifies in _decimalsOffset()).

Let's walk through an example. By way of reminder, here is what the variables above mean:

• totalSupply() = total number of shares issued
• totalAssets() = the balance of assets held by the ERC4626
• assets = the amount of assets the user is depositing

The formula is

shares_received = assets_deposited * totalSupply() / totalAssets();

There is some implementation details for rounding in favor of the pool and adding 1 to totalAssets() to ensure we don't divide by zero if the pool is empty.

Let's say we have the following numbers:

assets_deposited = 1,000

totalSupply() = 1,000

totalAssets() = 999,999 (the formula adds 1, so we will set it this way to make the number nice)

In that case, the shares the user will get is 1,000 x 1,000 ÷ 1,000,000, or exactly 1.

This is obviously very fragile. If the attacker frontruns the deposit of 1,000 shares and deposits assets, then the victim will get zero back, because 1 million divided by a number larger than 1 million is zero in integer division.

How does virtual liquidity solve this? Using the code from the screenshot above, we would set _decimalOffset() to be 3, so that way totalSupply() gets 1,000 added to it.

Effectively, we are making the numerator 1,000 times larger. This forces the attacker to make a donation 1,000 times as large, which disincentivizes them from conducting the attack.

Example of inflation attack

1. When a depositor wants to be the initial depositor, sends 10 USDC to the vault.
2. Attacker see’s that tx and front runs with calling deposit with 1 USDC. So, now the attacker becomes the initial depositor and totalSupply becomes 1. Attacker receives 1 share.
3. And now attacker donates equal amount of USDC that user transfer to the vault without calling the deposit function. So, the totalSupply won’t be updated. totalSupply still 1. And the totalBalance becomes 10 USDC.
4. Now the else block of the deposit executes and number of shares that mints to the user becomes 0.
5. So, the shares are that minted are only to attacker. So attacker owns the whole ownership on vault. Attacker can withdraw all the balance in the vault now.

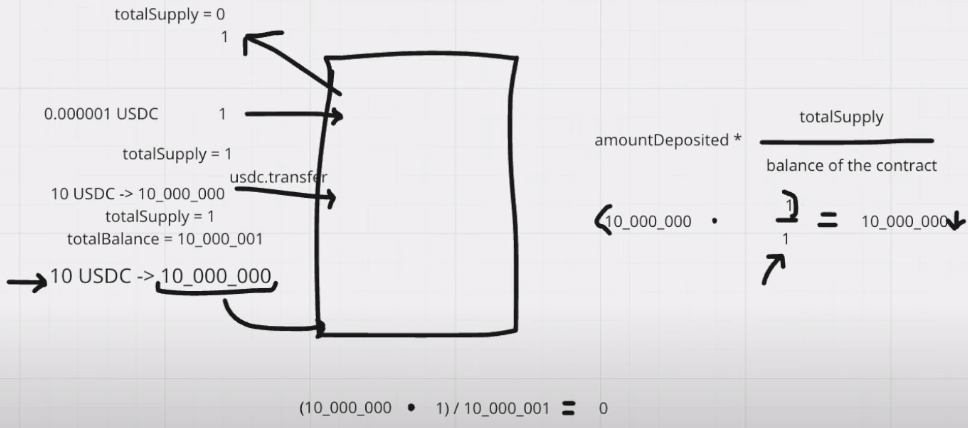
Example Implementation of share/asset calculation

Real life examples of share / asset accounting

Earlier versions of Compound minted what they called c-tokens to users who supplied liquidity. For example, if you deposited USDC, you would get a separate cUSDC (Compound USDC) back. When you decided to stop lending, you would send back your cUSDC to compound (where it would be burned) then get your pro-rata share of the USDC lending pool.

Uniswap used LP tokens as “shares” to represent how much liquidity someone had put into a pool, (and how much they could withdraw pro-rata) when they redeemed the LP tokens for the underlying asset.

Chapter-2 : ERC3156 Flash Loans

Flash Loans and how to hack them: a walk through of ERC 3156

Flash loans are loans between smart contracts that must be repaid in the same transaction.

Simple Flash Loan :

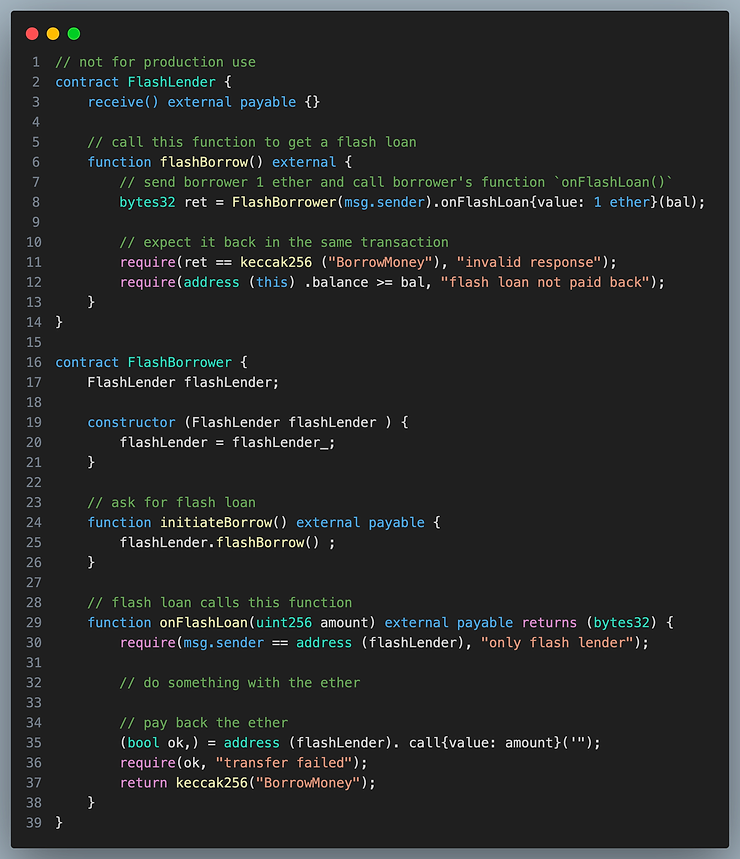
If the borrower does not pay back the loan, therequire statement with the message “flash not paid back” will cause the entire transaction to revert.

• Only contracts can work with flash loans
• No need of collateral to take flash loan

What are flashloans used for?

Arbitrage : The most common use case for a flash loan is to do an arbitrage trade.

Refinancing Loans

For regular DeFi loans, they typically require some kind of collateral. For example, if you were borrowing $10,000 in stable coins, you would need to deposit $15,000 of Ether as collateral.

If your stable coins loan had a 5% interest and you wanted to refinance with another lending smart contract at 4%, you would need to

1. pay back the $10,000 in stable coins
2. withdraw the $15,000 Ether collateral
3. deposit the $15,000 Ether collateral into the other protocol
4. borrow $10,000 in stable coins again at the lower rate

This would be problematic if you had the $10,000 tied up in some other application. With a flashloan, you can do steps 1-4 without using any of your own stable coins.

Exchanging collateral

In the example above, the borrower was using $15,000 of Ether as collateral. But suppose the protocol is offering a lower collateralization ratio using wBTC (wrapped bitcoin)? The borrower could use a flash loan and a similar set of steps outline above to swap out the collateral instead of the principal.

Liquidating Borrowers

In the context of DeFi loans, if the collateral falls below a certain threshold, then the collateral can get liquidated — forcibly sold to cover the cost of the loan. In the example above, if the value of the Ether was to drop to $12,000, then the protocol might allow someone to purchase the Ether for $11,500 if they first pay back the $10,000 loan.

A liquidator could use a flash loan to pay off the $10,000 stable coin loan and receive $11,500. They would then sell this on another exchange for stable coins, and then pay back the flash loan.

Increase yield for other DeFi applications

Uniswap and AAVE earn depositors’ money through trading fees or lending interest. But since they have such a large amount of capital in one place, they can make additional money by also offering flash loans. This increases the efficiency of capital since the same capital now has more uses.

Hacking Smart Contracts

Flash loans are probably most famous for their use by black hat hackers to exploit protocols. The primary attack vectors for flash loans are price manipulation and governance (vote) manipulation. Used on DeFi applications with inadequate defense, flash loans allow attackers to heavily buy up an asset increasing its price, or acquiring a bunch of voting tokens to push through a governance proposal.

The following is a list of flash loan hacks for the curious. Vulnerability is two-sided however. A flash lending and flash borrowing contract can also be vulnerable to losing money if not implemented properly.

ERC3156 Protocol

ERC3156 seeks to standardize the interface for getting flash loans.

ERC3156 Receiver Specification

The first aspect of the standard is the interface the borrower needs to implement, which is shown below. The borrower only needs to implement one function.

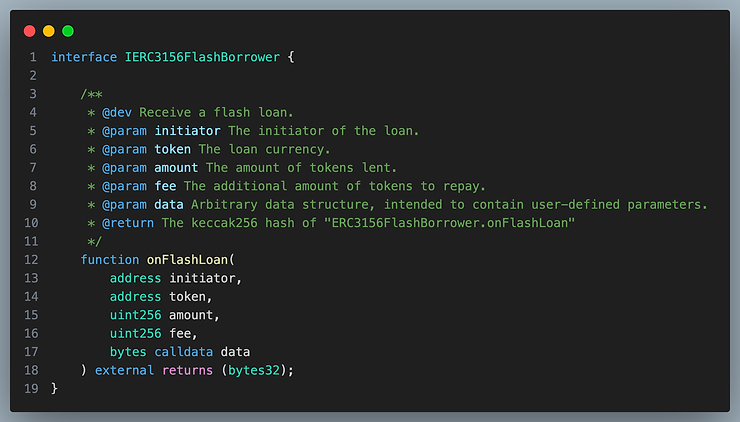
initiator

This is the address that initiated the flash loan. You probably want some kind of validation here so that untrusted addresses are not initiating flashloans on your contract. Usually, the address would be you, but you shouldn’t assume that!

The function onFlashLoan is expected to be called by the flash loan contract, not the initiator. You should check msg.sender is the flash loan contract inside the onFlashLoan() function because this function is external and anyone can call it.

Initiator is not msg.sender or the flash loan contract. It is the address that triggered the flash lending contract to call the receiver’s onFlashLoan function.

token

This is the address of the ERC20 token you are borrowing. Contracts offering flash loans will usually hold several tokens they can flash loan out. The ERC3156 flash loan standard does not support flash loaning native Ether, but this can be implemented by flash loaning WETH and having the borrower unwrap the WETH. Because the borrowing contract is not necessarily the contract that called the flash loaner, the borrowing contract may need to be told what token is being flash lent.

fee

Fee is how much of the token needs to be paid as a fee for the loan. It is denominated in absolute amount, not percentages.

data

If your flash loan receiving contract isn’t hard coded to take a particular action when receiving a flash loan, you can parameterize its behavior with the data parameter. For example, if your contract is arbitraging trading pools, then you would specify which pools to trade with.

return value

The contract must return keccak256("ERC3156FlashBorrower.onFlashLoan")

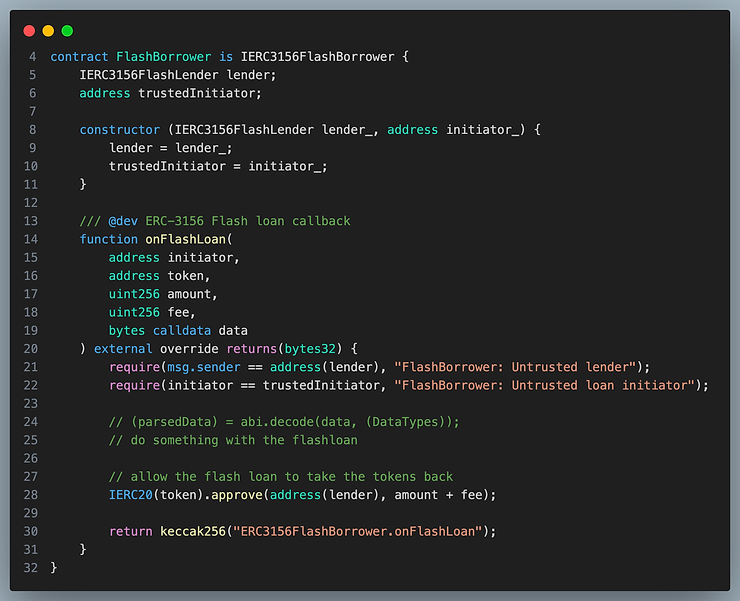
Reference implementation of the borrower

If the flash lender were somehow compromised, the contract below could be exploited through feeding it bogus amount and fee and initiator data. If the lender is immutable, this isn’t a concern, but it could be an attack vector if the lender is upgradeable.

ERC3156 Lender Specification

Below is the interface for the lender specified by ERC3156

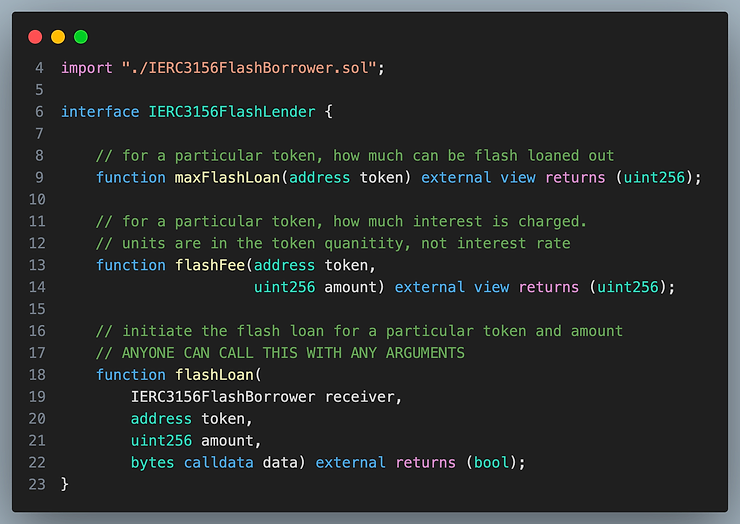
The flashLoan() function needs to accomplish a few important operations:

• Someone might call flashLoan() with a token the flash loan contract does not support. This should be checked for.
• Someone might call flashLoan() with an amount that is larger than maxFlashLoan. This also should be checked for
• data is simply forwarded to the caller.

More importantly, flashLoan() must transfer the tokens to the receiver and transfer them back. It should not rely on the borrower transferring the tokens back for repayment.

Reference Implementation of Lender

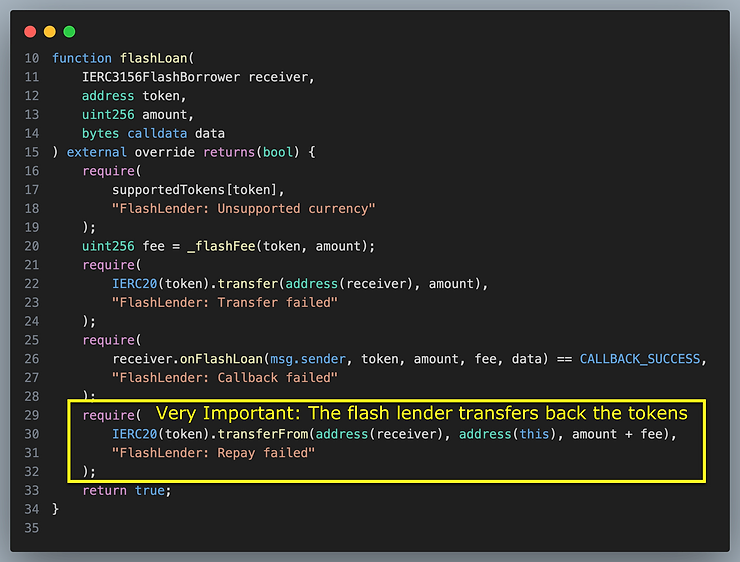
Note that the reference implementation is assuming that the ERC20 tokens return true on success, which not all do, so use the SafeTransfer library if using non-compliant ERC20 tokens.

Security Considerations

Access control and input validation for borrower

The borrowing smart contract must have the controls in place to only allow the flash lender contract to be the caller of onFlashLoan(). Otherwise, some actor other than the flash lender can call onFlashLoan() and cause unexpected behavior.

Furthermore, anyone can call flashloan() with an arbitrary borrower as the target and pass arbitrary data. To ensure the data is not malicious, a flash loan receiver contract should only allow a restricted set of initiators.

Reentrance locks are very important

ERC 3156 by definition cannot follow the check effects pattern to prevent reentrancy. It has to notify the borrower it has received the tokens (make an external call), then transfer the tokens back. As such, nonReentrant locks should be added to the contract.

It is important that the lender is the one transferring the tokens back or that reentrancy locks are in place.

In the above implementations, the lender transfers the tokens back from the borrower. The borrower does not transfer the loans to the lender. This is important to avoid “side entrances” where the borrower deposits money into the protocol as a lender. Now the pool sees it’s balance has returned to what it was before, but the borrower suddenly has become a lender with a large deposit.

UniswapV2’s flash loan does not transfer the tokens back after the flash loan finishes. However, it uses a reentrancy lock to ensure that the borrower cannot “pay back the loan” by depositing it back into the protocol as if they were a lender.

For the borrower, ensure only flash lender contract can call onFlashLoan

The flash lender is hardcoded to only call the receiver’s onFlashLoan() function and nothing else. If a borrower had a way to specify which function the flash lender would call, then the flash loan could be manipulated into transferring other tokens in it’s possession (by calling ERC20.transfer) or granting approval to it’s token balance to a malicious address.

Because such actions require an explicit call to an ERC20 transfer or approve, this can’t happen if the flash lender can only call onFlashLoan().

Using token.balanceOf(address(this)) can be manipulated

In the implementation above, we do not use balanceOf(address(this)) except to determine the maximum flash loan size. This can be altered by someone else directly transferring tokens to the contract, interfering with the logic. The way we know the flash loan was paid back is because the lender transferred back the loan amount + fee. There are valid ways to use balanceOf(address(this)) to check repayment, but this must be combined with reentrancy checks to avoid paying back the loan as a deposit.

Why the flash borrower needs to return keccak256("ERC3156FlashBorrower.onFlashLoan");

This handles the situation where a contract (not the flash lender contract) with a fallback function has given approval to the flash lending contract. Someone could repeatedly initiate a flashloan with that contract as a recipient. Then the following would happen:

1. The victim contract gets a flashloan
2. The victim contract gets called with onFlashLoan() and the fallback function is triggered but does not revert. The fallback function responds to any function call that doesn't match the rest of the functions in the contract, so it will respond to a onFlashLoan() call.
3. The flash lender withdraws tokens from the borrower + fee

If this operation happens in a loop, the victim contract with the fallback will get drained. The same could happen with an EOA wallet, since calling a wallet address with onFlashLoan does not revert.

Checking that the onFlashLoan function does not revert isn’t good enough. The flash lender also checks that the value keccack256("ERC3156FlashBorrower.onFlashLoan") is returned so that it knows the borrower intended to borrow the tokens and also pay back the fee.

Chapter-3 :Uniswap V2 Architecture

Uniswap V2 Architecture: An Introduction to Automated Market Makers

Uniswap is a DeFi app that enables traders to swap one token for another in a trustless manner. It was one of the early automated market makers for trading (though not the first).

Automated market makers are an alternative to an order book, which the reader is assumed to already be familiar with.

How AMM works?

AMM

An automated market maker holds two tokens (token X and token Y) in the pool (a smart contract). It allows anyone to withdraw token X from the pool, but they must deposit an amount of token Y such that the ”total” of assets in the pool does not decrease, where we consider the “total” to be the product of the amounts of the two assets.

Assets are provided to the pool by liquidity providers, who receive so-called LP tokens to represent their share of the pool. Liquidity provider balances are tracked in a manner similar to how ERC 4626 works. The difference between an AMM and ERC 4626 is that ERC 4626 only supports one asset but an AMM has two tokens. Just like a vault, the liquidity providers’ share of the pool stays the same, but the product X*Y gets larger, so their slice is larger.

Advantages of AMMs

AMMs do not have a bid-ask spread

In an AMM, price discovery is automatic. It’s determined by the ratio of assets in the pool.

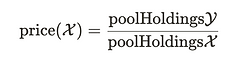
There is no need to wait for a suitable “bid” or “ask” order to show up. It always exists.

If there is a mismatch between the price in an AMM and another exchange, then a trader will arbitrage the difference, bringing the prices back into balance.

AMMs doubled as an oracle

Since the price of the assets is automatically determined, other smart contracts can use an AMM as a price oracle. However, AMM prices can be manipulated with flash loans, so safeguards need to be put in place when using AMMs in this manner. Nonetheless, it is valuable that price data is provided for free.

AMMs are highly gas efficient compared to order books

Order books requires a significant amount of bookkeeping (no pun intended). An AMM only needs to hold two tokens and transfer them according to simple rules. This makes them more efficient to implement.

Disadvantages of AMMs

There are two major drawbacks to automated market makers: 1) the price always moves and 2) impermanent loss for liquidity providers.

Even small orders move the price in AMMs

A buy or sell order will generally encounter more slippage than in an order book model, and the mechanism of swapping invites sandwich attacks.

Sandwich attacks are largely unavoidable in AMMs

1. Attacker’s first buy (front run): drives up price for victim

2. Victim’s buy: drive up price even further

3. Attacker’s sell: sell the first buy at a profit

Liquidity providers don’t have control over the price their assets are sold at

Liquidity providers can only provide assets proportional to the current ratio of tokens in the pool.

Liquidity providers for AMMs may suffer from impermanent Loss

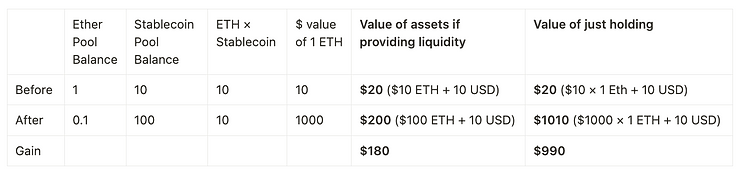
The missed out on gains are called “impermanent loss.” In the table above, the impermanent loss is $810 = ($990 - $180).

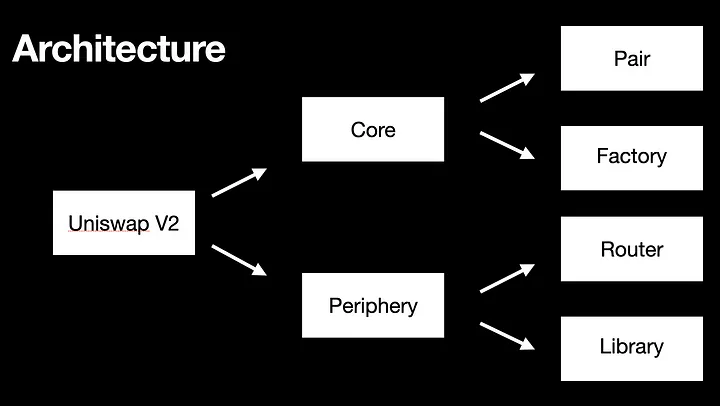
Architecture of Uniswap V2

The architecture of Uniswap V2 is surprisingly simple. At its core is the UniswapV2Pair contract that holds two ERC 20 tokens that traders can swap against, or liquidity providers can provide liquidity for. Every different possible UniswapV2Pair has a different UniswapV2Pair contract to manage it. If the desired UniswapV2Pair contract does not exist, a new one can be permissionlessly created from the UniswapV2Factory contract. UniswapV2Pair contracts are also ERC 20 tokens (they inherit from ERC 20), and that token is used to track deposits similar to how ERC 4626 works.

Although advanced traders or smart contracts can interact directly with a pair contract, most users will interact with a pair through a router contract, which has several convenience functions such as trading between pairs in one transaction to create a “synthetic” pair if it doesn’t exist.

There’s really only three smart contracts at play in the Uniswap V2 system.

Factory: github.com/Uniswap/v2-core/blob/master/contracts/UniswapV2Factory.sol

Pair: (which inherits ERC20): github.com/Uniswap/v2-core/blob/master/contracts/UniswapV2Pair.sol

Router: github.com/Uniswap/v2-periphery/tree/master/contracts

The core - periphery pattern

Observe that the router contract above is in a repository called “v2 periphery” and the pair is in the “v2 core” repository. Uniswap V2 follows the “core / periphery” design pattern where the most essential logic is held in the core while the “optional” logic is held in the periphery.

The intent behind this is to have the core hold as little code as possible, which reduces the possibility of bugs in the core business logic.

Uniswap V2 Core are the essential Uniswap V2 smart contracts, consisting of:

• UniswapV2ERC20.sol, contract is responsible for handling the LP tokens. It is a basic ERC20 contract, so we will not go over this.
• UniswapV2Pair.sol, which implements core swapping and liquidity provision functionality
• UniswapV2Factory.sol, which deploys UniswapV2Pair.sol contracts for any ERC20 token/ERC20 token pair

Uniswap V2 Periphery is an initial set of helpers, including:

• A router contract that performs the safety checks needed for safely swapping, adding, and removing liquidity.
• A migrator contract that can remove liquidity from Uniswap V1 and deposit it into Uniswap V2 in a single transaction.
• A library contract that can be used in the creation of other helper contracts.
• An example oracle contract that creates a simple TWAP from Uniswap V2 cumulative prices.
• An example flash swap contract that withdraws ERC20 tokens, executes arbitrary code, and then pays for them.

How to locate a pool, given two token addresses

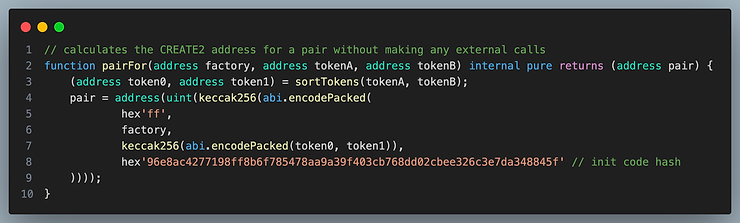
Instead of accessing a mapping from token pairs to pool address, smart contracts calculate the address of the pool by predicting the create2 address as a function of the token addresses and the factory address. Since there is no storage access, this is very gas efficient. Below is the helper function provided by UniswapV2Library for calculating the address of the Pair contract.

Why not use clones

The EIP 1167 clone pattern is used to create a collection of similar contracts, so why not use that here? Although the deployment would be cheaper, it would introduce an extra 2,600 gas per transaction due to the delegatecall. Since pools are intended to be used frequently, the cost savings from deployment would eventually be lost after a few hundred transactions, so it is worth deploying a pool as a new contract.

Chapter - 4 :Uniswap V2 Swap Function

Breaking Down the Uniswap V2 Swap Function.

UniswapV2Pair.sol#swap() : https://github.com/Uniswap/v2-core/blob/ee547b17853e71ed4e0101ccfd52e70d5acded58/contracts/UniswapV2Pair.sol#L159

• Line 170-171 directly transfers out the amount of tokens that the trader requested in the function arguments. There is no place inside the function where tokens are transferred in. But this does not mean we can just call swap and drain all the tokens we want to!

• The reason we can remove tokens right away is so that we can do flash loans. Of course, the require statement on line 182 (orange arrow) will require us to pay back the flash loan with interest.

• At the top of the function, there is a comment which says the function should be called from another smart contract which implements important safety checks. That means this function in particular is missing safety checks.

• The variables _reserve0 and _reserve1 are read on lines 161, 176-177, and 182, but they are not written to in this function.

  • _reserve0: Reserves of token x prior to the swap.

  • _reserve1: Reserves of token y prior to the swap.

• Line 182 (orange arrow) does not strictly check if X × Y = K. It checks if balance1Adjusted × balance2Adjusted ≥ K. This is the only require statement that does something “interesting.” The other require statements check that values aren’t zero or that you aren’t sending the tokens to their own contract address.

  • balance0Adjusted: Reserves of x after the trader sends tokensX to the pool minus 0.3% of the amount sent.

  • balance1Adjusted: Reserves of y after the tokensY are sent to the trader from the pool minus 0.3%.

• balance0 and balance1 are directly read from the actual balance of the pair contract using ER20 balanceOf.

• Line 172 (below the yellow box) is only executed if data is non-empty, otherwise it is not executed

We can use Swap() function for :

• Flash Loan

• Swapping one token for other

Flash Borrowing

Users do not have to use the swap function for trading tokens, it can be used purely as a flash loan.

The borrowing contract simply requests the amount of tokens they wish to borrow (A) without collateral and they will be transferred to the contract (B).

The data that should be provided with the function call is passed in as a function argument (C), and this will be passed to a function that implements.

IUniswapV2Callee. The function uniswapV2Call must pay back the flash loan plus the fee or the transaction will revert.

Swap

If a flash loan is not used, the incoming tokens must be sent as part of calling the swap function.

It should be clear that only a smart contract is able to interact with a swap function, because an EOA cannot simultaneously send the incoming ERC20 tokens and call swap in one transaction without the aid of another smart contract.

Measuring the amount of incoming tokens

The way Uniswap V2 “measures” the amount of tokens sent in is done on line 176 and 177.

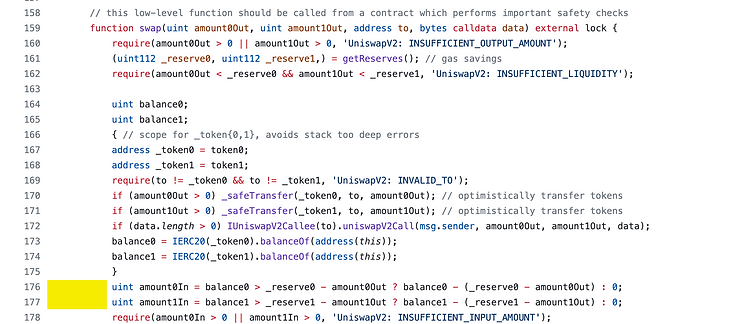
• _reserve0 and _reserve1 are not updated inside this function.

• They reflect the balance of the contract before the new set of tokens were sent in as part of the swap.

One of two things can happen for each of the two tokens in the pair:

1. The pool had a net increase in the amount of a particular token.

2. The pool had a net decrease (or no change) in the amount of a particular token.

The way the code determines which situation happened with the following lines:

uint amount0In = balance0 > _reserve0 - amount0Out ? balance0 - (_reserve0 - amount0Out) : 0;
uint amount1In = balance1 > _reserve1 - amount1Out ? balance1 - (_reserve1 - amount1Out) : 0;

The above two lines were doing the following thing

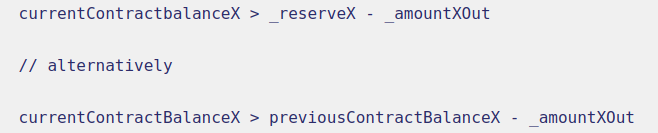
If it measures a net decrease, the ternary operator returns zero, otherwise it will measure the net gain of tokens in.

Simply,

• If the a token (0 or 1) ************************************is sent, the amount in to corresponding token will be amountXIn = balanceX - (_reserveX - amountXOut)
• If no token is sent amountXIn will become zero.

It is always the case that _reserveX > amountXOut because of the require statement on line 162.

Balancing XY = K

Now that we know how many tokens the user sent in, let’s see how to enforce XY = K.

Uniswap V2 charges a hardcoded 0.3% per swap, which is why we see the numbers 1000 and 3 at play.

reserve0 - Balance of token0 before swap

balance0 - Balance of token0 after swap

reserve1 - Balance of token1 before swap

balance1 - Balance of token1 after swap

balance0Adjusted - Updated balance of token0(X) minus 0.3% fee.

balance1Adjusted - Updated balance of token1(Y) minus 0.3% fee.

The line 182 is checking the following condition.

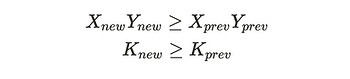
Particularly, doing this with fee.

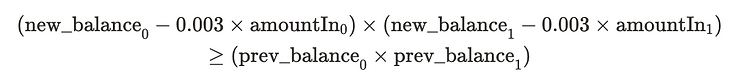
K is not really a constant

• Think about it this way, if someone donated tokens to the pool and changed the value of K

• Uniswap V2 doesn’t prevent you from “paying too much” i.e. transferring in too many tokens in during the swap (this is related to one of the safety checks)

• require statement is reverts if the loss the of the pool(K)

Accounting fot Fee

• But not only do we want K to get larger, we want it to get larger by at least an amount that enforces the 0.3% fee.

• Fee only applies to the tokens that go in, not on the tokens that go out.

  • Suppose we put in 1000 of token0 and remove 1000 of token1. We would need to pay a fee of 3 on token0 and no fee on token1.

  • Suppose we borrow 1000 of token0 and do not borrow token1. We are going to have to put 1000 of token0 back in, and we will have to pay a 0.3% fee on that — 3 of token0.

• Observe that if we flash borrow one of the tokens, it results in the same fee as swapping that token for the same amount. You pay fees on tokens in, not on tokens out.

• But if you don’t put tokens in, there is no way for you to borrow or swap.

Updating Reserves

Now that the trade is completed, then the “previous balance” must be replaced with the current balance. This happens in the call to the _update() function at the end of swap().

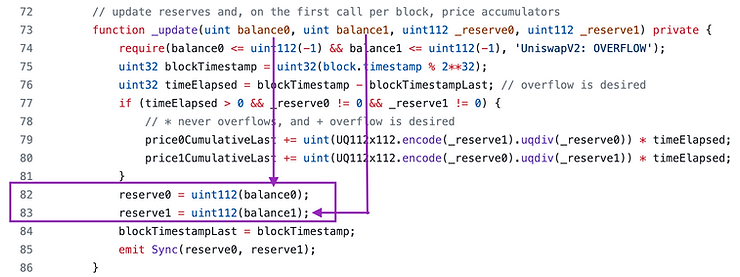
There is a lot of logic here to handle the TWAP oracle, but all we care about for now is lines 82 an 83 where the storage variables reserve0 and reserve1 are updated to reflect the changed balances. The arguments _reserve0 and _reserve1 are used to update the oracle, but they are not stored.

Safety Checks in Swap

There are two things that can go wrong:

1. The amountIn is not enforce to be optimal, so the user might overpay for the swap

2. AmountOut has no flexibility as it is supplied as a parameter argument. If the amountIn turns out to not be sufficient relative to amountOut, the transaction will revert and gas will be wasted.

These circumstances can happen if someone frontruns a transaction (intentionally or not) and changes the ratio of assets in the pool in an undesirable direction.

Example on swap

- Swap Function: swap()
***********************
- The swap() function is used by traders to swap tokens
- The swap function ensures that the amount of token you are swapping to is greater than zero (It can be any of the tokens in the pair contract) : Only one of the tokens can have value greater than zero at a time.
- It also ensures that the amount of token you are swapping from and the amount of token you are swapping to is less than the available reserve: hence it will throw an INSUFFICIENT LIQUIDITY error.

- If this checks are passed, it checks which of the amount out (amount0Out or amount1Out) that is greater than zero, then it transfers the amount out to the trader optimistically.

- Note: without making sure that the trader has already transferred corresponding tokens into our balance. We can optimistically transfer tokens out because the swap function have assertions later in the function to check if we received corresponding tokens (the Periphery contract should send in the tokens to the pair contract before calling it for the swap). If the pair contract have not received any tokens, assertions will fail and Solidity will revert the entire function.

- The code: if (data.length > 0) IUniswapV2Callee(to).uniswapV2Call(msg.sender, amount0Out, amount1Out, data);
will inform the receiver about the swap if requested

- Then it will check how many tokens was received by the pair contract.

- amount0In = balance0 > _reserve0 - amount0Out ? balance0 - (_reserve0 - amount0Out) : 0
- amount1In = balance1 > _reserve1 - amount1Out ? balance1 - (_reserve1 - amount1Out) : 0

Let's assume:
- reserve0 = 1000
- reserve1 = 500

A user is swapping 100 token0
This means the user will get 50 token1

token0 incoming = 100
token1 incoming = 0

token0 outgoing = 0
token1 outgoing = 50

At this point: 
balance0 = 1100
balance1 = 450

Using this formula:
- amount0In = balance0 > _reserve0 - amount0Out ? balance0 - (_reserve0 - amount0Out) : 0
- amount1In = balance1 > _reserve1 - amount1Out ? balance1 - (_reserve1 - amount1Out) : 0

amount0In = 1100 > 1000 - 0 ? 1100 - (1000 - 0) : 0

amount0In = 100

amount1In = 450 > 500 - 50 ? 450 - (500 - 50) : 0
amount1In = 0

- If the amountIn of either tokens of the pair contract is less than zero, it will revert with: INSUFFICIENT_INPUT_AMOUNT and the entire function will revert and nothing will have taken place.

- If the checks passes, then it proceeds to where the 0.3% fee paid by traders is calculated. It does this calculation to check and ensure that the fee was paid. Note the fee is also transferred to the pair contract and this is made possible by the Router contract.

- This is calculated by:
- balance0Adjusted = (balance0 * 1000) - (amount0In * 3)
- balance1Adjusted = (balance1 * 1000) - (amount1In * 3)

Remember:
balance0 = 1100
balance1 = 450

- balance0Adjusted = (1100 * 1000) - (100 * 3)
- balance0Adjusted = 1100000 - 300
- balance0Adjusted = 1099700

- balance1Adjusted = (450 * 1000) - (0 * 3)
- balance1Adjusted = 450000 - 0
- balance1Adjusted = 450000

- Then it checks if the k value (x*y=k) has decreased after the trade. The k value can never decrease because otherwise, Uniswap would lose from the swap.
**
require(balance0Adjusted.mul(balance1Adjusted) >= uint(_reserve0).mul(_reserve1).mul(1000**2), 'UniswapV2: K');
**

Remember k = x*y

adjustedK = balance0Adjusted * balance1Adjusted
previousK = (_reserve0 * _reserve1) * 1000^2 

adjustedK = 1099700 * 450000
adjustedK = 494865000000

previousK = (1000 * 500) * 1000^2
previousK = 500000000000

(The 1000^2 is because we multiplied balance0 and balance1 by 1000 when calculating the balance0Adjusted and balance1Adjusted)

- Finally, the _update() function is called to update the known reserves with the new balances and emit a Swap event.

Chapter - 5 : Mint and Burn Functions

• Useful : https://flow.com/engineering-blogs/uniswap-v2-explained-beginner-friendly

The lifecycle of Uniswap V2 is someone mints LP tokens (supplies liquidity, i.e. tokens to the pool) for the first time, then a second depositor mints liquidity, swaps happen, then eventually the liquidity providers burn their LP tokens to redeem the pool tokens.

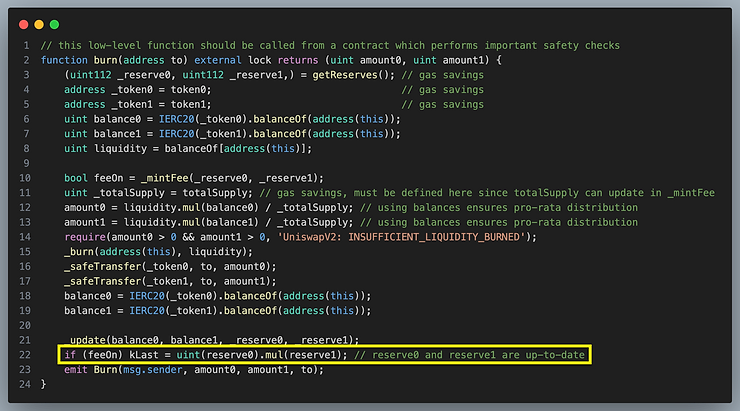
Uniswap V2 Burn

Before liquidity tokens can be burned, there needs to be liquidity in the pool, so let’s make that assumption. We assume that there are two tokens in the system: token0 and token1.

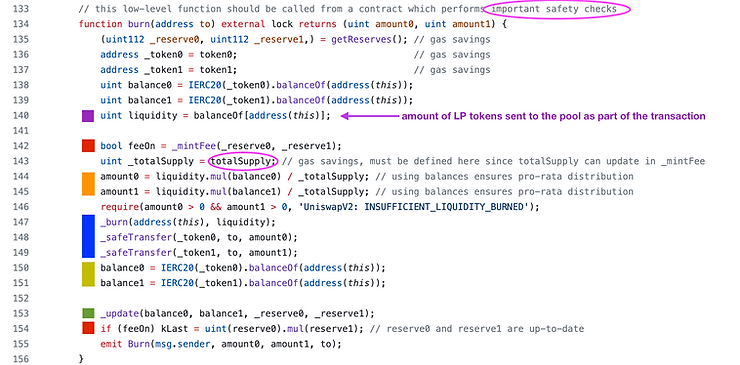
• On line 140 (purple box), liquidity is measured by the amount of LP tokens owned by the pool contract.

• It is assumed that the burner sent in LP tokens before calling burn, but advisably as part of one transaction. (If they are sent as two transactions, someone else can burn your LP tokens and remove your liquidity!)

• The amount the user sent to the contract will be burned. In general, we can assume that the contract will have zero balance of LP tokens, because if LP tokens are just sitting in the pair contract, someone will burn them and claim some of the token0 and token1 for free.

The red boxes on lines 142 and 154 denote fees, we will skip those for now as Uniswap does not apply fees to liquidity providers.

The orange boxes on lines 144 to 145 are where the amounts that the LP provider will get back are calculated. If the total supply of liquidity tokens is 1,000, and they burn 100 LP tokens, then they get 10% of the token0 and token1 held by the pool. Liquidity / totalSupply is their burned share of the total supply of LP tokens.

The blue box on line 147 to 149 is where the LP tokens are actually burned and the token0 and token1 are sent to the liquidity provider.

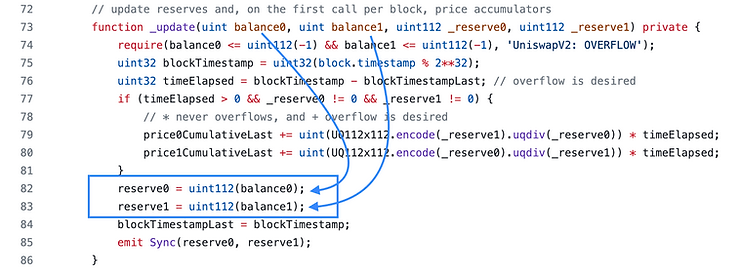
The (yellow box) on lines 150-151 updates balance variables so that the call to _update on line 153 (green box) can update the _reserve variables. Aside from updating the TWAP, the _update function simply updates the _reserve variables.

lock modifier

The lock modifier prevents reentrancy attack by setting the initial value of unlocked state variable to 1. Once a function with lock modifier is executed, the unlocked state variable value will be set to 0. To reenter the contract, the unlocked state variable is required to be == 1, thus preventing reentrancy. The unlocked state variable value will return to 1 upon successful execution of the function or failed execution (reversion to original state). Uniswap applies the lock modifier to all the UniswapV2Pair functions that perform external calls, such as mint, burn, swap and skim. Essentially this function modifier prevents 2 different parts of this contract to be executed simultaneously.

Safety checks in burn

The amount of token0 and token1 that the liquidity provider gets depends on the ratio of the LP tokens they burn to the total supply of LP tokens. However, the totalSupply can change before the burn transaction is confirmed. This means that the contract interacting with burn needs to implement slippage checks.

Example burn

- Burn Function: burn()
***********************

- The burn() function is the exact opposite of the mint() function
- The same gas saving mechanism is used just like in the mint() function
- balance0 and balance1 are total balances of the pair tokens in this pool

- balance0 = IERC20(_token0).balanceOf(address(this))
- balance1 = IERC20(_token1).balanceOf(address(this))
- liquidity = balanceOf[address(this)];

- liquidity is the amount of pool ownership tokens that the liquidity provider (who wishes to cash out) has. 

--- QUESTION ---
- But Why do we access the liquidity as the balance of address(this)? 

--- ANSWER ---
- Because the liquidity was transferred to the Pair contract by the Periphery (Router) contract before calling the burn function.

- The amount of token to withdraw to the liquidity provider is proportional to the amount of Pool Ownership tokens (LP tokens) he has and this is calculated by:
- amount0 = (liquidity * balance0) / totalSupply
- amount1 = (liquidity * balance1) / totalSupply

- After the amount is calculated, the burn function is called, which burns the LP token of the liquidity provider that was transferred into the contract from the contract.
- Then it transfers the pair token the the liquidity provider used in providing liquidity. (This transfer also includes the accumulated rewards from traders fees over time)
- The _update() function is called again which updated the reserves(reserve0 and reserve1) with the new balance (balance0 and balance1) after the pair tokens (token0 and token1) + the rewards have been transferred to the liquidity provider that removed their liquidity.

reserve0 = 1000
reserve1 = 500

balance0 = 1000
balance1 = 500

liquidity = 706
totalSupply = 1706

amount0 = liquidity.mul(balance0) / _totalSupply;

amount0 = (706 * 1000) / 1706
amount0 = 706000 / 1706
amount0 = 413.8335
amount0 = 413

amount1 = liquidity.mul(balance1) / _totalSupply;
amount1 = (706 * 500) / 1706
amount1 = 353000 / 1706
amount1 = 206.91676
amount1 = 206

balance0 = 1000 - 413
balance0 = 587

balance1 = 500 - 206
balance1 = 294

reserve0 = 587
reserve1 = 294

kLast = 172578

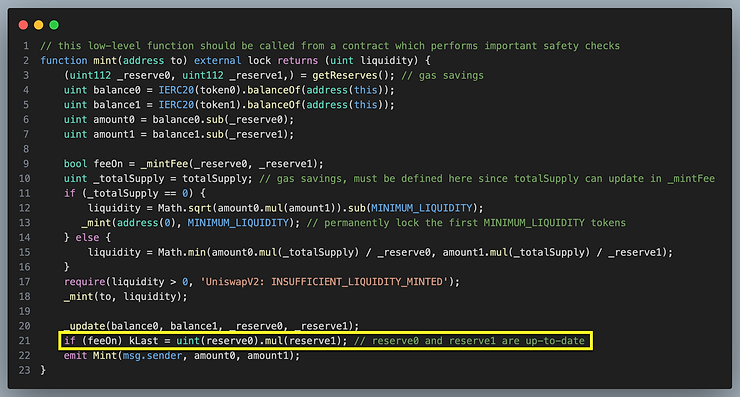
Uniswap V2 Mint

Here is the mint liquidity function. Much of the functionality is similar to burn.

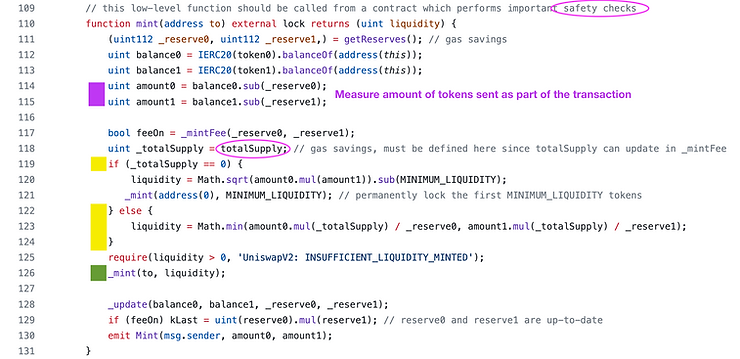
Uniswap V2 mint function deals two different cases when minting liquidity.

1. Minting liquidity when the pool is not empty

2. Minting initial liquidity. i.e, pool is empty

Minting liquidity when the pool is not empty

The liquidity that is credited to the user, and later minted to them on line 126 (green box), is the lesser of two values.

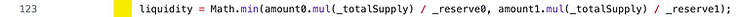
The ratio that line of code is measuring is amount0 / _reserve0 — scaled by the totalSupply of LP tokens.

Let’s say there are 10 token0 and 10 token1. If the user supplied 10 token0 and 0 token1 they will get the minimum of (10/10, 0/10) and get zero liquidity tokens back!

Another example: if they increase the supply of token0 by 5% and token1 by 10%, they will only get minted 5% of the supply of LP tokens (remember, this ratio is scaled by _totalSupply which is the current supply of LP tokens).

The fact that the user will get the worse of the two ratios (amount0 / _reserve0 or amount1 / _reserve1) they provide incentivizes them to increase the supply of token0 and token1 without changing the ratio of token0 and token1.

If the ratio is not the same as what the pool currently has, then there are always some tokens wasted in the sense that those tokens were added to the pool but no additional liquidity tokens were minted to the liquidity provider.

With this rule, the liquidity providers are incentivized to add tokens at the same ratio as the pool. And we know the rate is always close to the market price otherwise Arbitrageurs will arbitrage if the token ratio was off the market.

Why enforce this? Let’s say the pool currently has 100 of token0 and 1 of token1, and the supply of LP tokens is 1. Let’s say the total value, in dollars, of both tokens is $100 each, so the total value of the pool is $200.

If we took the maximum of the two ratios, someone could supply one additional token1 (at a cost of $100) and raise the pool value to $300. They’ve increase the pool value by 50%. However, under the maximum calculation, they would get minted 1 LP tokens, meaning they own 50% of the supply of the LP tokens, since the total circulating supply is now 2 LP tokens. Now they control 50% of the $300 pool (worth $150) by only depositing $100 of value. This is clearly stealing from other LP providers.

Supply Ratio Safety Check

The user might try to respect the token ratios, but if another transaction executes in front of them and changes the balance of token 0 to token 1, then they will get fewer liquidity tokens back than they expected.

Uniswap doesn't require exact amounts because otherwise the transaction would likely revert. Another transaction executed first would change the requirement between when the minter sent the transaction and when it was included in the block.

TotalSupply safety check

Just like the burn case, the totalSupply of LP tokens could change at the time, so some slippage protection must be implemented.

Minting liquidity when the pool is empty (First Minting)

Uniswap uses a special case when minting for the first time in pool to mitigate the inflation attack by using the MINIMUM_LIQUIDITY.

This is locked by sending the Mininum Liquidity to address(0) : Once this is done, the total supply can never be reduced to zero again even if the liquidity providers remove their liquidity from the pool. A brand new pool needs to lock in MINIMUM_LIQUIDITY amount of pool ownership (LP) token to avoid division by zero in the liquidity calculations.

MINIMUM_LIQUIDITY is 10**3. It may be possible to prevent indiscriminate proliferation of pairs, but in fact, it burns. Since 1000 burns, it means that MINIMUM_LIQUIDITY must be exceeded.

Example of inflation attack

Why Uniswap Calculates Liquidity as Square Root K

The more interesting question is why Uniswap V2 takes the square root of the product of the tokens supplied to calculate the amount of LP shares to mint.

It would seem that we could mint an arbitrary amount of tokens to the first LP — they own 100% of the shares (minus what was burned), so what difference does it make if it is scaled by 0.01 or 100?

Example: Doubling Liquidity

Let’s suppose we didn’t measure liquidity with the square root function and we start with 10 of token0 and 10 of token1 in the pool. Later on, the pool has 20 of token0 and 20 of token1 in the pool.

Intuitively, did the liquidity double or quadruple? Because if we don’t take the square root, liquidity would start at 100 (10 × 10) and end up at 400 (20 × 20). Arguably, liquidity did not quadruple. At first, the maximum of token0 you could obtain was (asymptotically) 100, but after the growth in liquidity, the “depth” of the liquidity for that token doubled, not quadrupled.

But how does this matter if future liquidity providers are not calculating liquidity using the square root while minting or burning? We saw new liquidity providers are “forced” to supply assets at the current rate, and burners can only redeem at the current rate — no square roots are involved.

The answer lies in how Uniswap would have collected fees from LPs if it chose to do so.

Example mint:

- Mint Function: mint()
***********************

- If the pool is a brand new pool,
- Liquidity is calculated using:
- liquidity = Math.sqrt( (amount0 * amount1) - MINIMUM_LIQUIDITY )

reserve0 = 0
reserve1 = 0
balance0 = 1000 // amount of token0 sent (Shiba)
balance1 = 500 // amount of token1 sent (Doge)

amount0 = 1000 - 0
amount1 = 500 - 0

amount0 = 1000
amount1 = 500

_totalSupply = 0
MINIMUM_LIQUIDITY 10 ^ 3

liquidity = Math.sqrt( (1000 * 500) - 1000)
liquidity = Math.sqrt(499000)
liquidity = 706.399320498
liquidity = 706

totalSupply = 706 + 1000
totalSupply = 1706

After this, reserves are updated and kLast is updated too
reserve0 = 1000
reserve1 = 500
kLast = 500000

- If the pool is not brand new
- Liquidity is calculated using:
- liquidity = Math.min( (amount0 * _totalSupply) / _reserve0, (amount1 * _totalSupply) / _reserve1 )

Fees

Going back to our earlier example of the pool growing from 100 of token0 and 100 of token1, to 200 of each, the profit of the liquidity provider is 100%, so they should pay a fee proportional to that amount. If we measured the size of the pool from 100 to 400, then they would have to pay fees on quadruple profit.

Uniswap opts to charge fees during liquidity removal because charging a protocol fee during swapping would increase the gas cost of a very common operation.

Uniswap V2 never actually turned on the protocol fee, so this discussion is a bit theoretical.

Chapter - 6 : Protocol Mint Fee

Uniswap V2 was designed to collect 1/6th of the swap fees to the protocol. Since a swap fee is 0.3%, 1/6th of that is 0.05%, so 0.05% of every trade would go to the protocol.

Although this feature was never actually activated, this feature anyway since some forks may use it. The fee is paid to feeTo address in LP Tokens.

Collecting protocol fees during swaps is inefficient

It would be inefficient to collect 0.05% of the fee on every trade because that would require additional token transfers.Therefore, the fee is collected when a liquidity provider calls burn or mint. Since these operations are infrequent compared to swapping tokens, this will lead to gas savings. To collect the mintFee, the contract calculates the amount of fees collected since that last happened, and mints enough LP tokens to the beneficiary address such that the beneficiary is entitled to 1/6th of the fee.

fee - the 0.3% collected from traders during the swap

mintFee - the 1/6th of the 0.3% fee.

Liquidity(L) is the square root of the products of the token balances in the pool. sqrt(K).

Computing the mintFee assumptions

For this to work, Uniswap V2 relies on the following two invariants:

• If mint and burn are not called, the liquidity of the pool can only increase.
• The increase in liquidity is purely due to fees (or donations).

By measuring the increase in liquidity since the last mint or burn, the pool knows how much fees were collected.

Calculation of mintFee

Suppose at t₁ the pool starts at 10 token0 and 10 token1.

After a lot of trading and fee collection, the new pool balance is 40 token0 and 40 token1 at t₂.

Liquidity is measured as the square root of the product of the two tokens, i.e. liquidity = sqrt(xy). The liquidity was 10 at t₁ and 40 at t₂, sqrt(100) and sqrt(1600) respectively. We are going to charge a fee on the growth from 10 to 40.

Specifically, 3/4ths, or 30 units of liquidity of the pool is due to fees. We want to mint enough LP tokens, the “mintFee” such that the beneficiary receives 1/6th of the “fee portion” of the pool. That is, they should be entitled to 5 units of liquidity (30 / 6).

Remember, the mint fee is dilutive. We mint more such that the proportional ownership of the liquidity providers is reduced.

The key insight is the invariant

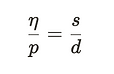
That is, if the mintFee η can redeem the amount of liquidity due to the protocol 𝑝, then the original LP supply 𝑠 can redeem the rest of the pool 𝑑.

• current liquidity after fees ℓ₂ is rootK

• previous liquidity is kLast

• the supply of LP tokens before dilution s is totalSupply

• the function is state changing, it mints the mintFee inside the function rather than return the calculation of the mintFee (blue highlight)

• the fee can be switched on an off with the flag feeOn which we haven’t discussed yet

Or simply,

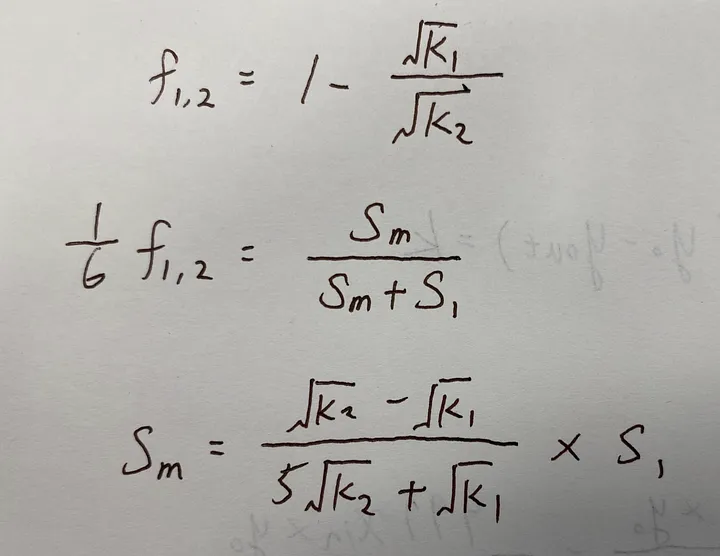
_mintFee is doing what exactly the same the above formulae.

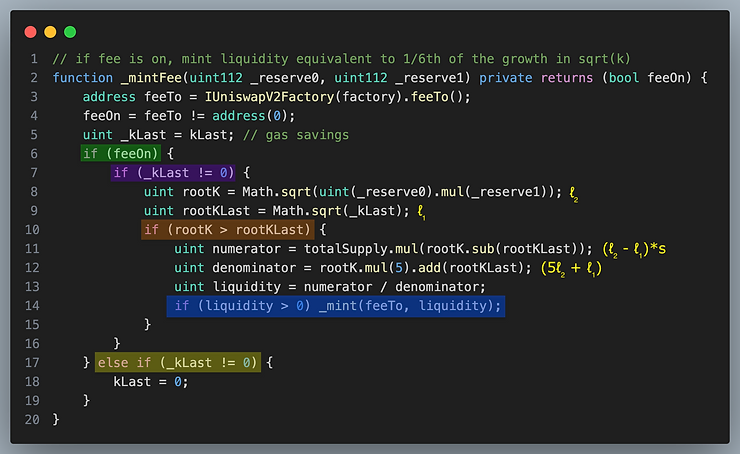
Where klast gets updated

In the code above, kLast is not set unless feeOn is switched to false. It is set at the completion of mint and burn but not swap because we are interested in measuring the growth of fees due to swaps between liquidity deposit and withdrawal events.

mint function

burn function

Explaination

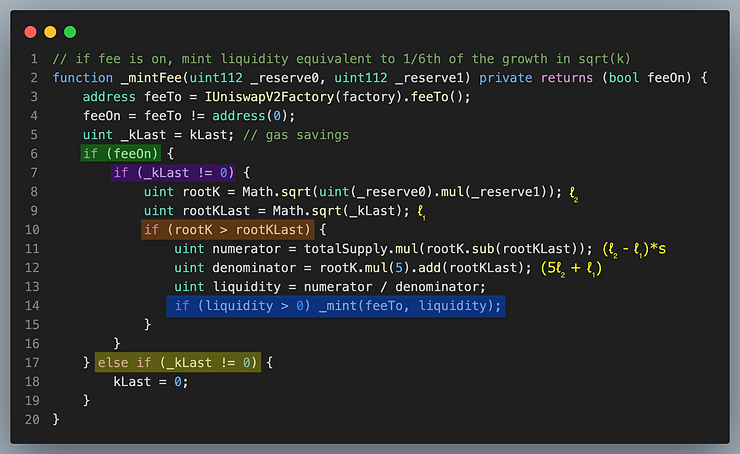
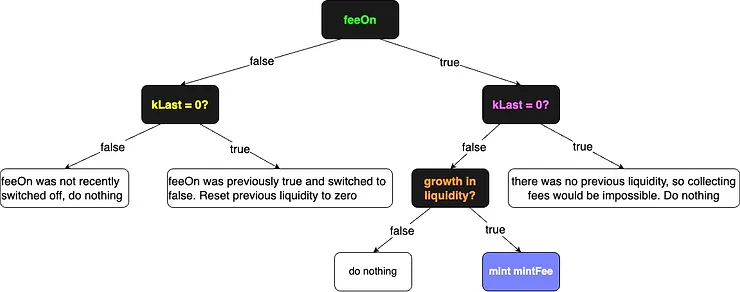
Let’s consider the possibilities in the code snippet above, repeated for convenience.

1. The feeOn is false, nothing is minted (green highlight)

2. The feeOn is false, kLast is zero (yellow highlight)

3. The feeOn is false, kLast is not zero (yellow highlight)

4. The feeOn is true, but there was no growth in liquidity (orange highlight)

5. The feeOn is true, and there was liquidity growth (orange highlight), so the mint fee applies (blue highlight)

It’s easier to see the logic in a decision tree, so here is the decision tree with the branches colored the same as the if statements.

Example

Asumming:
reserve0 = 1000
reserve1 = 500
klast = 1000 * 500
klast = 500000

new liquidity:
token0 100
token1 50

currentReserve0 = 1000 + 100 = 1100
currentReserve1 = 500 + 50 = 550

rootK = Math.sqrt(currentReserve0 * currentReserve1)
rootK = Math.sqrt(605000)
rootK = 777.8174593052 (round down)
rootK = 777

rootKLast = Math.sqrt(_kLast);
rootKLast = Math.sqrt(500000);
rootKLast = 707.1067811865
rootKLast = 707

kDifference = rootK - rootKLast
kDifference = 777.8174593052 - 707.1067811865
kDifference = 70.7106781187
kDifference = 70

using totalSupply = 499000 (s1)

numerator = totalSupply * kDifference
numerator = 499000 * 70
numerator = 34930000

denominator = (rootK * 5) + rootKLast
denominator = (777 * 5) + 707
denominator = 3885 + 707
denominator = 4592

liquidity = numerator / denominator
liquidity = 34930000 / 4592
liquidity = 7606.7073170732 (round down)
liquidity = 7606 (This liquidity goes to Uniswap: feeTo address)

7606 amount of LP Tokens to feeTo address

Chapter - 7 : TWAP Oracle

Time Weighted Average Price

What exactly Price in Uniswap ?

Suppose we have 1 Ether and 2,000 USDC in a pool. This implies that the price of Ether is 2,000 USDC. Specifically, the price of Ether is 2,000 USDC / 1 Ether (ignoring decimals).

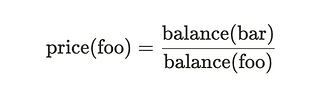
In the example above, it is saying “how may bars do you need to pay to get one foo” (ignoring fees).

Price is a ratio

Because price is a ratio, they need to be stored with a data type which has decimal points (which Solidity types do not have by default).

That is, we say Ethereum is 2000 and USDC (in price of Ethereum) is 0.0005 (this is ignoring decimals of both assets).

Uniswap uses a fixed point number with 112 bits of precision on each side of the decimal, this takes up a total of 224 bits, and when packed with a 32 bit number, it uses up a single slot.

**UQ112x112is a library for supporting floating numbers** since solidity does not support floating numbers default(floats are larger than integer so it will cost more gas fee). The last 112 bits is for fractional part.

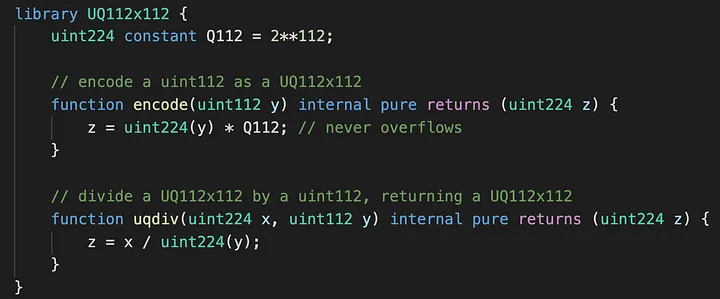
This library sets Q112 to 2¹¹². There are two functions, encode and uqdiv(decode).

encode takes argument y and times it with Q112 while uqdiv divides a UQ112x112 by a uint112 and returns a UQ112x112.

But why 112?

• Since there is an unsigned type using uint224, 112 bits represent the previous significant digit, and the remaining 112 is the exponent. 112 + 112 = 224, and usually unsigned is 256, so 32 bits if subtracted from each other!

• Expresses 32 bits as time.

• The remaining 32 bits are used as time, which is used in UTC notation. Since people have been around for a long time, cast to uint32(time) form for UTC-based time and truncate it. Only look at the last one and use the interval difference using under/over flow in between.

• 2^32 - 1 second is very long. So, if 2^10 is 1000 and (10^3)^3, it takes almost 110 years.

• Since there is unsigned 32bit, since the Robust Price Oracle Price is a rational expression, UQ112.112 is used.

Oracle definition

An oracle in computer science terms is a “source of truth.” A price oracle is a source of prices. Uniswap has an implied price when holding two assets, and other smart contracts can use this as a price oracle.

The intended users of the oracle are other smart contracts, since other smart contracts can easily communicate with Uniswap to determine the price, but getting price data from an off-chain exchange would be a lot harder.

However, just taking the ratio of the balances to get the current price isn’t safe.

Motivation behind TWAP

• Measuring price at a single point of time may be prone to flash loan attack. That is an attacker could a huge amount of flash loan which leads to drastic change in price of the asset in the pool.

• This may lead uninted behaviour in the contract that uses this price.

The Uniswap V2 oracle defends against this in two ways:

1. It provides a mechanisms for consumers of the price (usually smart contracts) to take the average a previous time period (decided by the user). This means an attacker has to constantly manipulate the price for several blocks, which is a lot more costly than using a flash loan.

2. It doesn’t incorporate the current balance into the oracle calculation

This should prone to price manipulation attacks.

• If the asset does not have much liquidity, or the time window of taking the average is not sufficiently large, then a well-resourced attacker can still prop up the price (or suppress the price) long enough to manipulate the average price at the time of measurement.

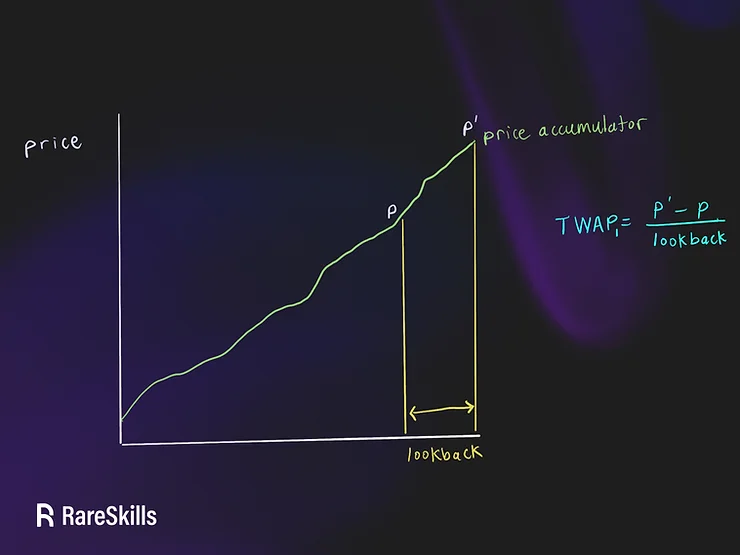
How TWAP works

A TWAP (Time Weighted Average Price) is the average of the price for the specified time interval.

Example:

Over the last day, the price of an asset was $10 for the first 23 hours and $11 for the most recent one. The expected average price should be closer to $10 than $11, but it will still be in between those values. Specifically, it will be ($10 * 23 + $11 * 1) / 24 = $10.0417

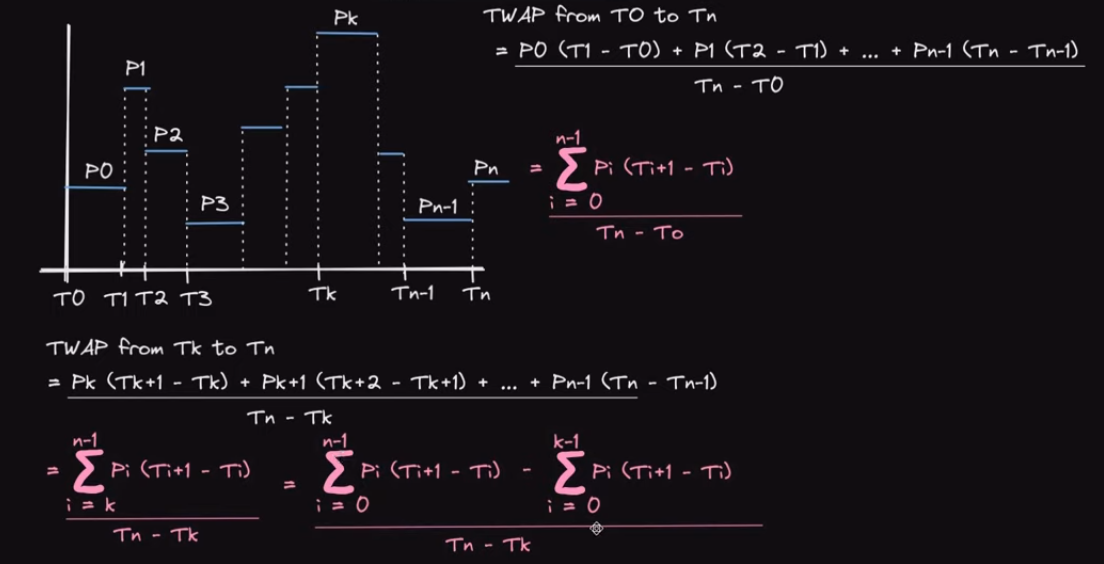
Uniswap V2 does not store lookback or the denominator

In our example above, we only looked at prices for the last 24 hours, but what if you care about prices for the last hour, week, or some other interval? Uniswap of course cannot store every look back that someone might be interested, and there also isn’t a good way to consistently snapshot the price as someone would have to pay for the gas.

The solution is that Uniswap only stores the numerator of values — every time a change is the liquidity ratio happens (mint, burn, swap, or sync are called), it records the new price and how long the previous price lasted.

The variables price0Cumulativelast and price1CumulativeLast are public, so an interested party needs to snapshot them.

• price0CumulativeLast and price1CumulativeLast are only updated on line 79, 80 there is no way to decrease them.
• They always increase with every call to _update until they overflow.

Limiting the lookback window

We dont want the average price since the pool deployed. We want price in a certain amount of time.

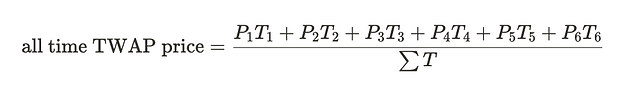
If we are only interested in prices since T4, then we want to be doing the following

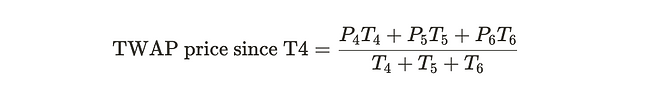
We can get this part of the TWAP since the priceXCumulative keeps tracks from the pool deployement.

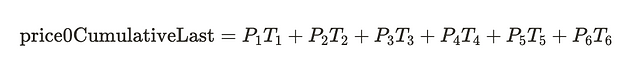
We need to isolate the part we want.

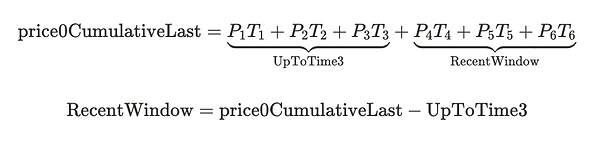
If we can able to snapshot the price at the end of T3, we get the value UpToTime3 .

Now we can get the cumulative price of the recent window by calculating

price0Cumulativelast - UpToTime3then

If we divide this value by the time of the recent window. We will get the price average for the recent window of time.

This is what we are doing.

Only calculating the last 1 hour TWAP in Solidity

If we want a 1 hour TWAP, we need to anticipate that we will need a snapshot of the accumulator one hour from now. So we need to access the public variable price0CumulativeLast and the public function getReserves() to get the last update time, and snapshot those values

After at least 1 hour has passed, we can call getOneHourPrice() and we will access the newest value of price0CumulativeLast from Uniswap V2.

Since the time we snapshotted the old price, Uniswap has been updating the accumulator.

We need to deploy a seperate contract that snapshots the cumulative prices of Uniswap to get the price for the interval of time that we want.

The following contrac is an example contract that calculates the average TWAP price of Token0 of a pool.

• The getOneHourPrice() needs to be called atlease after an hour of time passed afer calling snapshot()

• getOneHourPrice() can calculate price for not only just one hour, it can call for any time interval of (1 - 3) hours.

What if the last snapshot is over three hours ago?

The above contract will fail to give price when there is a case that update() function has no been called for over 3 hours .

Uniswap V2 function **_update** is called during mint, burn, and swap, but none of those interactions happen, then lastSnapshotTime will record a time from a while ago.

In result the the getTimeElapsed() will return time which is greater than 3 hours. So, the getOneHourPrice() will be reverted due the check of second require.

So, to solve this problem call the sync function at the time it does a snapshot, as that will internally call _update.

Why TWAP must track two ratios

The price of A with respect to B is simply A/B and vice versa. For example, if we have 2000 USDC in the pool (ignoring decimals), and 1 Ether, then the price of 1 Ether is simply 2000 USDC / 1 ETH.

The price of USDC, denominated in ETH, is simply that number with the numerator and denominator flipped.

However, we cannot just “invert” one of the prices to get the other when we are accumulating pricing. Consider the following. If our price accumulator starts at 2 and adds 3, we cannot just do one over the accumulator:

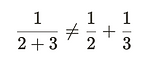
However, the prices are still “somewhat symmetric,” hence the choice of fixed point arithmetic representation must have the same capacity for the integers and for the decimals. If Eth is 1,000 times more “valuable” than a USDC, then USDC is 1,000 times “less valuable” than USDC. To store this accurately, the fixed point number should have the same size on both sides of the decimal, hence Uniswap’s choice of u112x112.

PriceCumulativeLast always increases until it overflows, then keeps going

Reason why Overflow desirable

Uniswap V2 was built before Solidity 0.8.0, thus arithmetic overflowed and underflowed by default. Correct modern implementations of the price oracle need to use the unchecked block to ensure everything overflows as expected.

Eventually, the priceAccumulators and the block timestamp will overflow. In that case, the previous reserve will be higher than the new reserve. When the oracle computes the change in price, they will get a negative value. However, this won’t matter due to the rules of modular arithmetic.

To make things simple let’s use an imaginary unsigned integers that overflow at 100.

We snapshot the priceAccumulator at 80 and a few transactions/blocks later the priceAccumulator goes to 110, but it overflows to 10. We subtract 80 from 10, which gives -70. But the value is stored as an unsigned integer, so it gives -70 mod(100) which is 30. That’s the same result we would expect if it didn’t overflow (110-80=30).

This is true of all overflow boundaries, not just 100 in our example.

Overflowing the timestamp or priceAccumulator does not cause issues because of how modular arithmetic works.

Overflowing the timestamp

The same thing happens when we overflow the timestamp. Because we are using a uint32 to represent it, there won’t be any negative numbers. Again, let’s assume we overflow at 100 for the sake of simplicity. If we snapshot at time 98 and consult the price oracle at time 4, then 6 seconds have passed. 4 - 98 % 100 = 6, as expected.

Chapter - 8 : UniswapV2Library

UniswapV2Library Code Walkthrough

The Uniswap V2 Library simplifies some interactions with pair contracts and is used heavily by the Router contracts. It contains eight functions that are not state-changing,. They are also handy for integrating Uniswap V2 from a smart contract.

Using UniswapV2Library

If you want to predict how much to put into or expect out of a trade, or a sequence of trades across pairs, the UniswapV2Library is the tool to

getAmountOut()

Given an input asset amount, returns the maximum output amount of the other asset (accounting for fees) given reserves.

Let x be the incoming token, y be the outgoing token, Δx be the amount coming in and Δy be the amount going out.

Δx = amountIn* 0.997 (with 0.3% fee on in coming tokens)

getAmountIn()

Returns the minimum input asset amount required to buy the given output asset amount (accounting for fees) given reserves.

pairFor() and sortTokens()

pairFor() Calculates the address for a pair without making any external calls. It deterministically derived from the addresses of the tokens and the address of the factory that deployed the pair using the create2 function.

sortTokens() sorts the order of tokens.

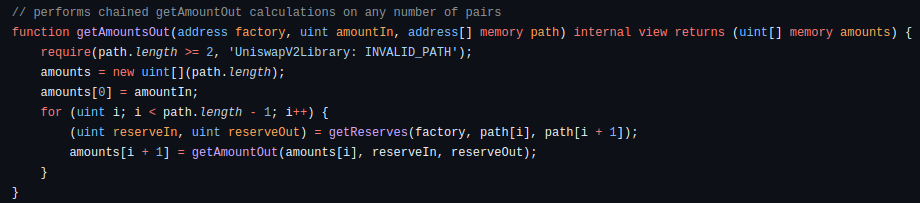
getAmountsOut

If a trader supplies a sequence of pairs, (A, B), (B, C), (C, D) and iteratively calls getAmountOut starting with a certain amount of A, then the amount of token D that will be received can be predicted.

• The smart contract doesn’t figure out the optimal sequence of pairs on its own, it needs to be told the list of pairs to calculate the chain of swaps over. This is best done off-chain.
• It doesn’t just return the final token amountOut in the chain, but the amount out at every step.

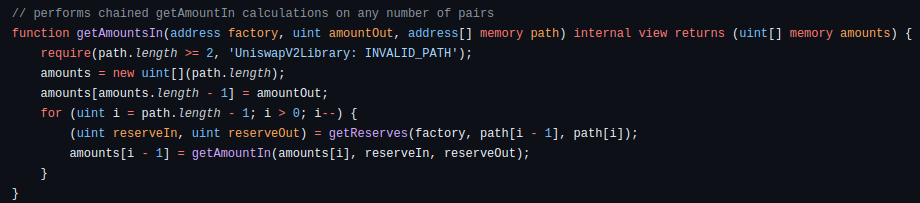
getAmountsIn

Does opposite to getAmountsOut

getReserves()

The function getReserves is simply a wrapper around the function getReserves from the Uniswap V2 pair contract except that it also removes the timestamp when the price was last updated.

Calls getReserves on the pair for the passed tokens, and returns the results sorted in the order that the parameters were passed in.

quote()

Given some asset amount and reserves, returns an amount of the other asset representing equivalent value.

This function returns the price of foo denominated in bar as of the last update. This function should be used with care as it is vulnerable to flash loan attacks.

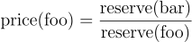
Chapter - 9 : Routers

Uniswap v2 router code walkthrough

The Router contracts provide a user-facing smart contract for

• safely minting and burning LP tokens (adding and removing liquidity)

• safely swapping pair tokens

• They add the ability to swap Ether by integrating with the wrapped Ether (WETH) ERC20 contract.

• They add the slippage related safety checks omitted from the core contract.

• They add support for fee on transfer tokens.

Router contracts part of v2-periphery contracts.

Router02 is everything Router01 does with support added for fee on transfer tokens

**UniswapV2Router01 should not be used any longer, because of the discovery of a low severity bug and the fact that some methods do not work with tokens that take fees on transfer.

The current recommendation is to use UniswapV2Router02.**

UniswapV2Router01

[UniswapV2Router01](https://github.com/Uniswap/v2-periphery/blob/master/contracts/UniswapV2Router01.sol) is deployed at 0xf164fC0Ec4E93095b804a4795bBe1e041497b92a on the Ethereum mainnet, and the Ropsten, Rinkeby, Görli, and Kovan testnets. It was built from commit 2ad7da2.

Functions:

1. swapExactTokensForTokens()

2. swapTokensForExactTokens()

3. swapExactETHForTokens()

4. swapTokensForExactETH()

5. swapExactTokensForETH()

6. swapETHForExactTokens()

7. _swap()

8. _addLiquidity()

9. addLiquidity()

10. addLiquidityETH()

11. removeLiquidity()

12. removeLiquidityETH()

13. removeLiquidityWithPermit()

14. removeLiquidityETHWithPermit()

15. Read only functions : factory(), WETH()

16. UniswapV2Library functions

swapExactTokensForTokens()

In swapExactTokensForTokens the "first token is exact" means that the amount of the input token you are swapping is a fixed quantity.

The first element of path is the input token, the last is the output token, and any intermediate elements represent intermediate pairs to trade through (if, for example, a direct pair does not exist).

In the case of swapExactTokensForTokens, the user specifies exactly how much of the first token they are going to deposit and the minimum amount of the output token they will accept.

For example, suppose we want to trade 25 token0 for 50 token1. If this is the exact price at the current state, this leaves no tolerance for the price changing before our transaction is confirmed, leading to a revert. So we instead specify the minimum out to be 49.5 token1, implicitly leaving a 1% tolerance.

**msg.sender should have already given the router an allowance of at least amountIn on the input token.**

swapTokensForExactTokens()

In swapTokensForExactTokens, the "second token is exact" indicates that the amount of the output token you want to receive is a fixed quantity.

In this case we specify we want exactly 50 token1, but we are willing to trade up to 25.5 token0 to obtain in.

Receive an exact amount of output tokens for as few input tokens as possible, along the route determined by the path.

**msg.sender should have already given the router an allowance of at least amountInMax on the input token.**

Which swap function to use?

Users using EOA will use swapExactTokensForTokens function. Because they can approve the exact amount of tokens that going to send. And the approve will revert when they dont receive specified minimum amount of tokens. By having an exact input, they can approve the exact amount.

Smart contracts integrating with Uniswap however may have more complex requirements, so the router gives them the option for both.

How swap works?

When the input is exact (swapExactTokensForTokens), the function predicts the expected output across a single swap or a chain of swaps. If the resulting output is below the user specified amount, the function reverts. Vice versa for exact output: it calculates the required input and reverts if it is above the user specified threshold.

Then both functions will transfer the user’s tokens to the pair (remember, Uniswap V2 Pair requires the tokens to be sent into the contract before the pair contract function swap is called). Finally, they both call the internal _swap function discussed next.

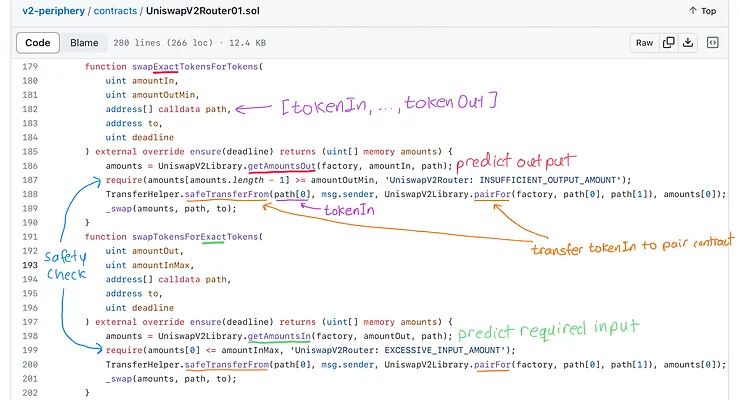
The _swap() function

Under the hood, all publicly facing functions with the name swap in the name call the _swap internal function shown below.

Recall that the function signature for the core swap function specifies the amountOut for both tokens and the amountIn is implied by the amount that was transferred in before the function was called.

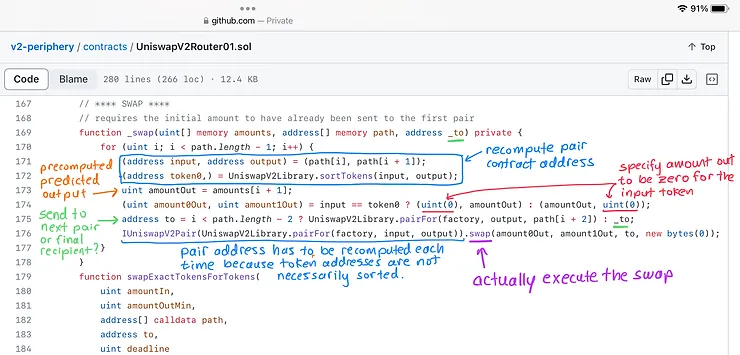
The new bytes(0) parameter means not to do a flashswap, which is usually executed when performing a canonical swap.

swapExactETHForTokens

Swaps an exact amount of ETH for as many output tokens as possible, along the route determined by the path. The first element of path must be WETH, the last is the output token, and any intermediate elements represent intermediate pairs to trade through (if, for example, a direct pair does not exist).

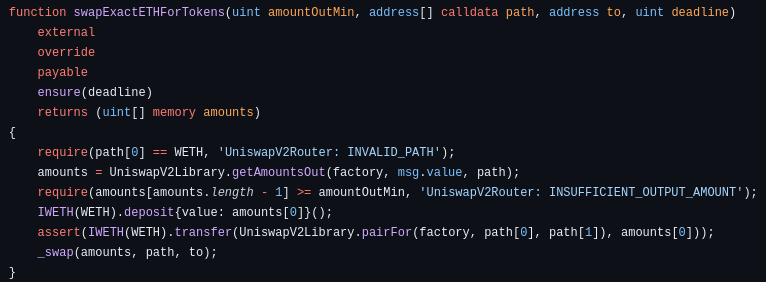
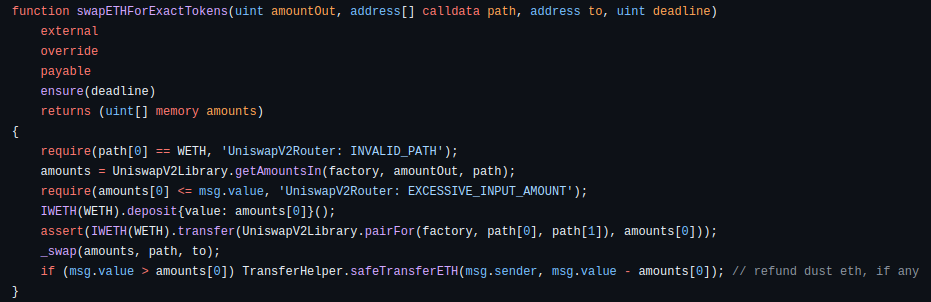
swapTokensForExactETH

Receive an exact amount of ETH for as few input tokens as possible, along the route determined by the path. The first element of path is the input token, the last must be WETH, and any intermediate elements represent intermediate pairs to trade through (if, for example, a direct pair does not exist).

• msg.sender should have already given the router an allowance of at least amountInMax on the input token.

• If the to address is a smart contract, it must have the ability to receive ETH.

swapExactTokensForETH

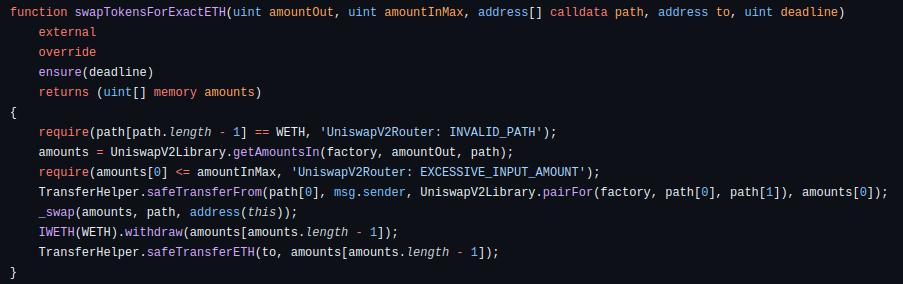
Swaps an exact amount of tokens for as much ETH as possible, along the route determined by the path. The first element of path is the input token, the last must be WETH, and any intermediate elements represent intermediate pairs to trade through (if, for example, a direct pair does not exist).

• If the to address is a smart contract, it must have the ability to receive ETH.

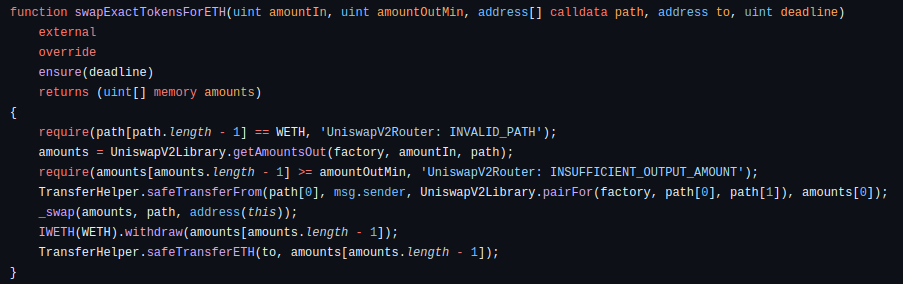
swapETHForExactTokens

Receive an exact amount of tokens for as little ETH as possible, along the route determined by the path. The first element of path must be WETH, the last is the output token and any intermediate elements represent intermediate pairs to trade through (if, for example, a direct pair does not exist).

• Leftover ETH, if any, is returned to msg.sender.

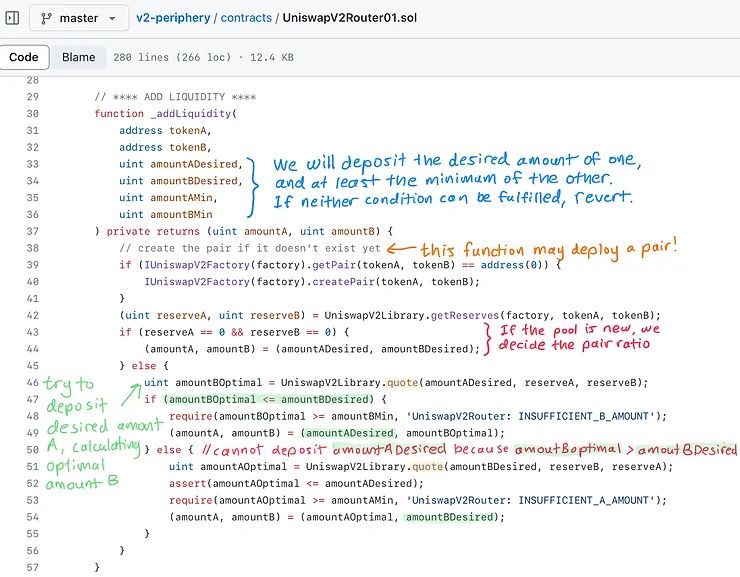
_addLiquidity

Safety checks for adding liquidity Specifically, we want to make sure we deposit the two tokens at exactly the same ratio as what the pair currently has, otherwise the amount of LP tokens we mint is the worse of the two ratios between what we provide and what the pair balances are. However, the ratio could change between when the liquidity provider attempts to add liquidity and when the transaction is confirmed.

To guard against this, a liquidity provider must provide (as a parameter), the minimum balance they are seeking to deposit for token0 and token1 (UniswapV2 calls those amountAMin and amountBMin). Then they transfer in an amount higher than those minimums (UnsiwapV2 calls those amountADesired and amountBDesired). If the pair ratio has shifted in such a way that the minimums are no longer respected, then the transaction reverts.

_addLiquidity will take amountADesired and calculate the correct amount of tokenB that will respect the ratio. If this is amount is higher than amountBDesired (the amount of B the liquidity provider sent), then it will start with amountBDesired and calculate the optimal amount of B. The logic is show below. Note that adding liquidity may create a new pair contract if it doesn’t already exist.

For example, suppose the current pair balance is 100 token0 and 300 token1. We want to add 20 and 60 token0 and token1 respectively, but the pair ratio might change. So we instead approve the router for 21 token0 and 63 token1 while saying the minimum we want to deposit is 20 and 60. If the ratio shifts such that the optimal amount of token0 to deposit is 19.9, then the transaction reverts.

Recall that we said quote should not be used as an oracle, and that is still true. However for the purposes of adding liquidity we are not interested in the average of previous prices but the current price (pool ratio) now because the liquidity provider must respect it.

addLiquidity() and addLiquidityEth()

These functions should be self-explanatory. They first calculate the optimal ratio using _addLiquidity from above then transfer the assets to the pair, then call mint on the pair. The only difference is the **addLiquidityEth** function will wrap the Ether into WETH first.

Removing Liquidity

Remove liquidity calls burn but uses parameters amountAMin and amountBMin (red highlights) as safety checks to ensure that the liquidity provider gets back the amount of tokens they are expecting. If the ratio of tokens changes dramatically before the the liquidity tokens are burned, then the user burning the tokens won’t get back the amount of token A or B that they are expecting.

The function removeLiquidityEth calls removeLiquidity (green highlight) but sets the router as the recipient of the tokens. The regular ERC20 token is then transferred to the liquidity provider, and the WETH is unwrapped to ETH, then sent back to the liquidity provider.

removeLiquidityWithPermit() and removeLiquidityETHWithPermit()

On line 109 in the file above with the gray comment send liquidity to pair, this step assumes the pair contract has approval to transfer LP tokens from the liquidity provider to burn them. This means burning the LP tokens requires approving the pair first. This step can be skipped with permit(), since the LP tokens of Uniswap V2 is an ERC20 Permit Token. The function removeLiquidityWithPermit() receives a signature to approve and burn in one transaction. If one of the tokens is WETH, the liquidity provider would use removeLiquidityETHWithPermit().

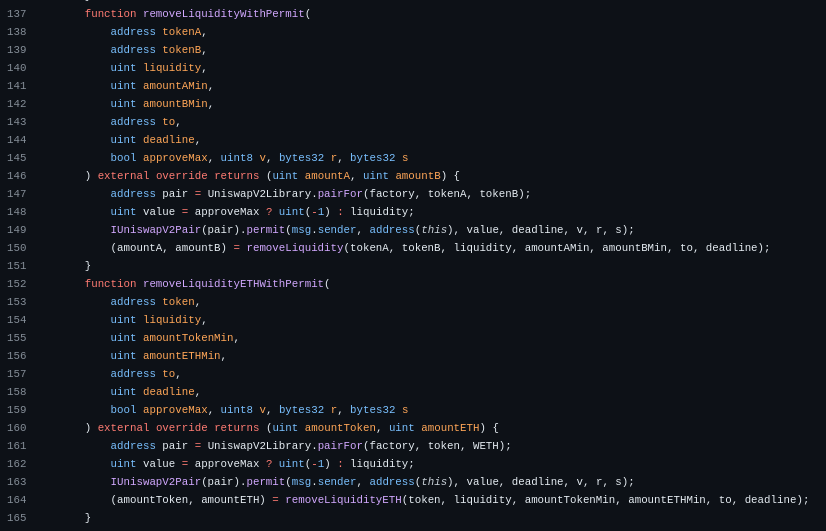
UniswapV2Router02

Because routers are stateless and do not hold token balances, they can be replaced safely and trustlessly, if necessary. This may happen if more efficient smart contract patterns are discovered, or if additional functionality is desired. For this reason, routers have release numbers, starting at 01. This is currently recommended release, 02.

UniswapV2Router02 is deployed at 0x7a250d5630B4cF539739dF2C5dAcb4c659F2488D on the Ethereum mainnet, and the Ropsten, Rinkeby, Görli, and Kovan testnets. It was built from commit 6961711.

Router02 : supporting fee on transfer tokens (tokens will take fees when any transfer of the token is performed).

To handle fee on transfer tokens, the router cannot directly do it’s calculations on arguments like amountIn (for swap) or liquidity (for removing liquidity). Adding liquidity is not affected by fee on transfer tokens because the user is only credited for what they actually transfer to the pair.

Functions:

Router1 + some extra.

1. _swapSupportingFeeOnTransferTokens()

2. swapExactTokensForTokensSupportingFeeOnTransferTokens()

3. swapExactETHForTokensSupportingFeeOnTransferTokens()

4. swapExactTokensForETHSupportingFeeOnTransferTokens()

5. removeLiquidityETHSupportingFeeOnTransferTokens()

6. removeLiquidityETHWithPermitSupportingFeeOnTransferTokens()

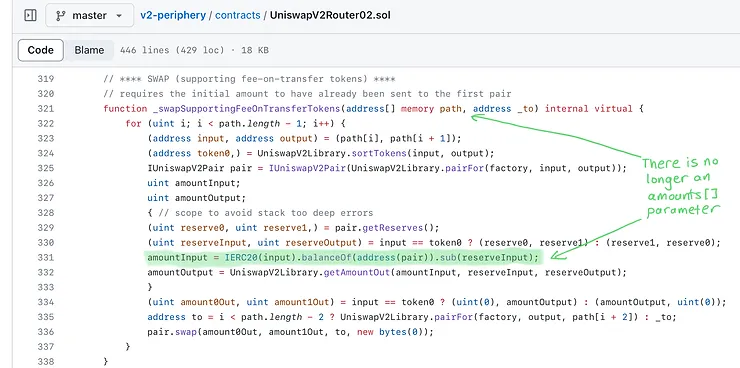
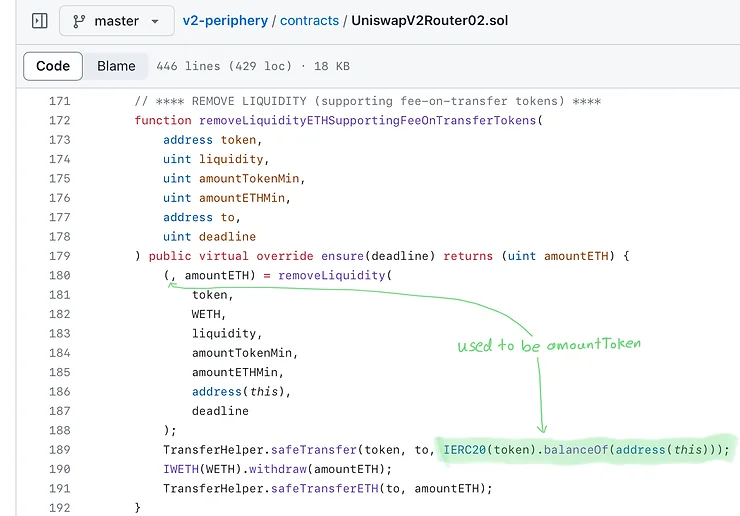
Wrappers around the UniswapV2Library

The rest of the functions in the Router library are wrappers around the UniswapV2Library functions as shown below.

Summary

The Router contracts provide a user-facing mechanism for swapping tokens with slippage protection, possibly across multiple pools, and add support for trading ETH and fee-on-transfer tokens (in Router02). Depositing liquidity does not need to account for fee-on-transfer tokens because Uniswap only credits for what was actually transferred into the pool.

The depositing liquidity functions ensure the user only deposits at the exact ratio of the pool. Removing liquidity can be as simple as transferring LP tokens to the router then burning them, or include unwrapping WETH and withdrawing fee on transfer tokens.

Chapter - 10 : MISC

UniswapV2Factory.sol

The factory contract is mainly responsible for creating new contract pairs (UniswapV2Pair.sol).

In order to concentrate liquidity, there can only be one smart contract per pair. In other words, if there is a WETH/UNI pair contract already, the factory won’t allow you to create the same pair. Of course, you can bypass that (by deploying the pair contract directly), but the core principle here is to concentrate liquidity as much as possible to avoid price slippage and have more liquidity.

Here is the function that creates pairs in UniswapV2Factory:

UniswapV2Migrator.sol

• Migrate liquidity from UniswapV1

• In order to transfer all the liquidity that was in Uniswap V1, they automatically withdrew and deposited in uniswap v2. But there has been a lot of Rug-pull?

  • My LP, because I handed over my authority, my entire property was hit by users whose credit was not guaranteed. In the end, malicious users tend to steal money and then launder it.

• Migration itself makes it easy to transfer liquidity, and it is difficult to change on the blockchain because it is difficult to transfer existing customers.

UniswapV2ERC20.sol

• Used for defining LP token.

• ERC20 wrap to EIP712 for using permit function

UniswapV2Pair.sol : sync() and skim()

skim and sync are needed when balances on the ERC20 contracts of the exchange tokens, fall out of sync with the reserve variables in the Pair contract. This can happen for example when someone just transfers some Dogecoin to Pair contract’s account for no reason. There are 2 solutions to keep reserve variables in sync with the actual balances on ERC20 contracts.

When liquidity is added in Uniswap v2 the reserves are updated. However, in a case where tokens are deposited in contract, the balance of the contract would vary from the amount of reserves. The trade performed while balances and reserves are not synced would have incorrect values. The function sync() sets the reserves of the contract according to the balances.

sync() functions as a recovery mechanism in the case that a token asynchronously deflates the balance of a pair. In this case, trades will receive sub-optimal rates, and if no liquidity provider is willing to rectify the situation, the pair is stuck. sync() exists to set the reserves of the contract to the current balances, providing a somewhat graceful recovery from this situation.

If the user deposits balance in the contract and this balance exceeds uint112. Calling the **sync**() function is not suitable. Since the **_update**() function in **sync**() uses uint112 which will overflow. In such a case the function **skim**() is to be used. Skim will remove the excess balance and resolve the deadlock of clogging the uint112.

skim() functions as a recovery mechanism in case enough tokens are sent to an pair to overflow the two uint112 storage slots for reserves, which could otherwise cause trades to fail. skim() allows a user to withdraw the difference between the current balance of the pair and 2**112 - 1 to the caller, if that difference is greater than 0.

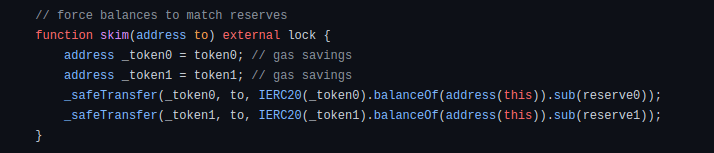
• It allows someone to withdraw the extra funds from the Pair contract. Anyone can call this function!

• The skim() function forces the balances to match reserves

• it transfers any extra token to the address that called the function

References

• Rareskills Uniswap V2 Book
• @0xOwneThurm AMM tutorial
• @ProgrammerSmart
• @Zer0luck.eth Blog
• @pessimistic_io Blogs
• AMM Integration tips by @officer_cia
• Uniswap Docs
• A Great Anon
• An Eilte Anon
• Great examples by a Ultimate guy